Principio de Arquímedes

El principio de Arquímedes afirma que todo cuerpo sumergido en un fluido experimenta un empuje vertical y hacia arriba igual al peso de fluido desalojado.
La explicación del principio de Arquímedes consta de dos partes como se indica en la figuras:

1. El estudio de las fuerzas sobre una porción de fluido en equilibrio con el resto del fluido.
2. La sustitución de dicha porción de fluido por un cuerpo sólido de la misma forma y dimensiones.

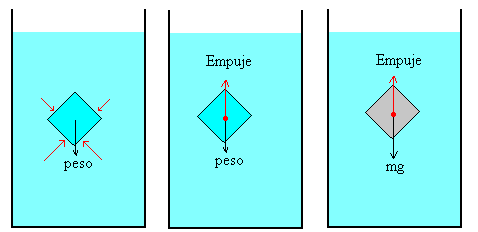
Porción de fluido en equilibrio con el resto del fluido.
Consideremos, en primer lugar, las fuerzas sobre una porción de fluido en equilibrio con el resto de fluido. La fuerza que ejerce la presión del fluido sobre la superficie de separación es igual a p·dS, donde p solamente depende de la profundidad y dS es un elemento de superficie.
Puesto que la porción de fluido se encuentra en equilibrio, la resultante de las fuerzas debidas a la presión se debe anular con el peso de dicha porción de fluido. A esta resultante la denominamos empuje y su punto de aplicación es el centro de masa de la porción de fluido, denominado centro de empuje.
De este modo, para una porción de fluido en equilibrio con el resto, se cumple
Empuje=peso=r_f·gV
El peso de la porción de fluido es igual al producto de la densidad del fluido r_f  por la aceleración de la gravedad g y por el volumen de dicha porción V.
Se sustituye la porción de fluido por un cuerpo sólido de la misma forma y dimensiones.
Si sustituimos la porción de fluido por un cuerpo sólido de la misma forma y dimensiones. Las fuerzas debidas a la presión no cambian, por tanto, su resultante que hemos denominado empuje es la misma y actúa en el mismo punto, denominado centro de empuje.
Lo que cambia es el peso del cuerpo sólido y su punto de aplicación que es el centro de masa, que puede o no coincidir con el centro de empuje.

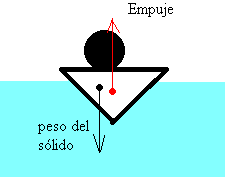Por tanto, sobre el cuerpo actúan dos fuerzas: el empuje y el peso del cuerpo, que no tienen en principio el mismo valor ni están aplicadas en el mismo punto.En los casos más simples, supondremos que el sólido y el fluido son homogéneos y por tanto, coinciden el centro de masa del cuerpo con el centro de empuje.

Ejemplo:

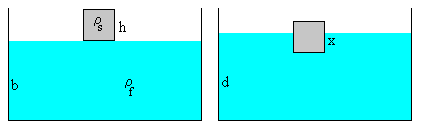
Supongamos un cuerpo sumergido de densidad ρ rodeado por un fluido de densidad ρ_f. El área de la base del cuerpo es A y su altura h.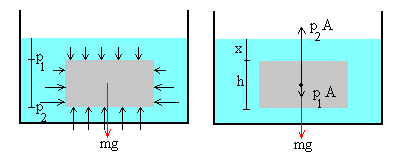

La presión debida al fluido sobre la base superior es p₁= ρ_fgx, y la presión debida al fluido en la base inferior es p₂= ρ_fg(x+h). La presión sobre la superficie lateral es variable y depende de la altura, está comprendida entre p₁ y p₂.

Las fuerzas debidas a la presión del fluido sobre la superficie lateral se anulan. Las otras fuerzas sobre el cuerpo son las siguientes:

• Peso del cuerpo, mg
• Fuerza debida a la presión sobre la base superior, p₁·A
• Fuerza debida a la presión sobre la base inferior, p₂·A

En el equilibrio tendremos que

mg+p₁·A= p₂·A
mg+ρ_fgx·A= ρ_fg(x+h)·A

o bien,

mg=ρ_fh·Ag

Como la presión en la cara inferior del cuerpo p₂ es mayor que la presión en la cara superior p₁, la diferencia es ρ_fgh. El resultado es una fuerza hacia arriba ρ_fgh·A sobre el cuerpo debida al fluido que le rodea.

Como vemos, la fuerza de empuje tiene su origen en la diferencia de presión entre la parte superior y la parte inferior del cuerpo sumergido en el fluido.

Con esta explicación surge un problema interesante y debatido. Supongamos que un cuerpo de base plana (cilíndrico o en forma de paralepípedo) cuya densidad es mayor que la del fluido, descansa en el fondo del recipiente.

Si no hay fluido entre el cuerpo y el fondo del recipiente ¿desaparece la fuerza de empuje?, tal como se muestra en la figura

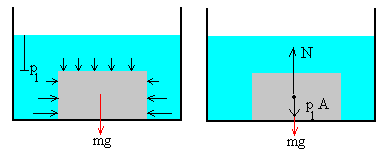
Si se llena un recipiente con agua y se coloca un cuerpo en el fondo, el cuerpo quedaría en reposo sujeto por su propio peso mg y la fuerza p₁A que ejerce la columna de fluido situada por encima del cuerpo, incluso si la densidad del cuerpo fuese menor que la del fluido. La experiencia demuestra que el cuerpo flota y llega a la superficie.

El principio de Arquímedes sigue siendo aplicable en todos los casos y se enuncia en muchos textos de Física del siguiente modo:

Cuando un cuerpo está parcialmente o totalmente sumergido en el fluido que le rodea, una fuerza de empuje actúa sobre el cuerpo. Dicha fuerza tiene dirección hacia arriba y su magnitud es igual al peso del fluido que ha sido desalojado por el cuerpo.

Energía potencial mínima.

En este apartado, se estudia el principio de Arquímedes como un ejemplo, de cómo la Naturaleza busca minimizar la energía.

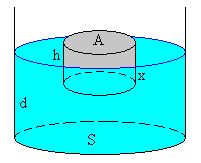Supongamos un cuerpo en forma de paralepípedo de altura h, sección A y de densidad ρ_s. El fluido está contenido en un recipiente de sección S  hasta una altura b. La densidad del fluido es ρ_f> ρ_s.

Se libera el cuerpo, oscila hacia arriba y hacia abajo, hasta que alcanza el equilibrio flotando sobre el líquido sumergido una longitud x.  El líquido del recipiente asciende hasta una altura d. Como la cantidad de líquido no ha variado S·b=S·d-A·x

Hay que calcular x, de modo que la energía potencial del sistema formado por el cuerpo y el fluido sea mínima.

Tomamos el fondo del recipiente como nivel de referencia de la energía potencial.

El centro de masa del cuerpo se encuentra a una altura d-x+h/2. Su energía potencial es E_s=(ρ_s·A·h)g(d-x+h/2)

Para calcular el centro de masas del fluido, consideramos el fluido como una figura sólida de sección S y altura d a la que le falta una porción de sección A y altura x.

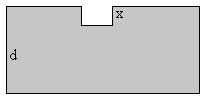
• El centro de masas de la figura completa, de volumen S·d es d/2
• El centro de masas del hueco, de volumen A·x, está a una altura (d-x/2)

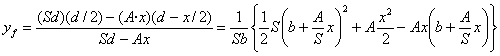
La energía potencial del fluido es E_f=ρ_f(Sb)g·y_f

La energía potencial total es E_p=E_s+E_f

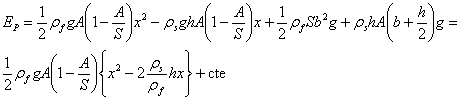
El valor de la constante aditiva cte, depende de la elección del nivel de referencia de la energía potencial.

En la figura, se representa la energía potencial E_p(x) para un cuerpo de altura h=1.0, densidad ρ_s=0.4, parcialmente sumergido en un líquido de densidad ρ_f=1.0.

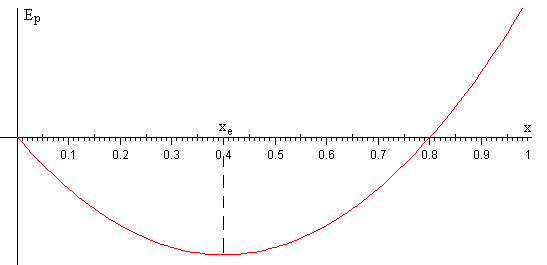
La función presenta un mínimo, que se calcula derivando la energía potencial con respecto de x e igualando a cero

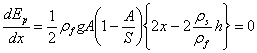
En la posición de equilibrio, el cuerpo se encuentra sumergido

Energía potencial de un cuerpo que se mueve en el seno de un fluido

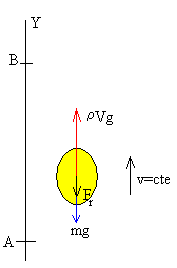Cuando un globo de helio asciende en el aire actúan sobre el globo las siguientes fuerzas: El peso del globo Fg=–mgj . El empuje Fe= rfVgj, siendo rf  la densidad del fluido (aire). La fuerza de rozamiento Fr debida a la resistencia del aire

Dada la fuerza conservativa podemos determinar la fórmula de la energía potencial asociada, integrando

• La fuerza conservativa peso F_g=–mgj está asociada con la energía potencial E_g=mg·y.
• Por la misma razón, la fuerza conservativa empuje F_e= rVg j está asociada a la energía potencial E_e=-r_fVg·y.

Dada la energía potencial podemos obtener la fuerza conservativa, derivando

La energía potencial asociada con las dos fuerzas conservativas es
E_p=(mg- r_fVg)y
A medida que el globo asciende en el aire con velocidad constante experimenta una fuerza de rozamiento F_r debida a la resistencia del aire. La resultante de las fuerzas que actúan sobre el globo debe ser cero.
r_f Vg- mg-F_r=0
Como r_fVg> mg a medida que el globo asciende su energía potencial  E_p disminuye.
Empleando el balance de energía obtenemos la misma conclusión

El trabajo de las fuerzas no conservativas F_nc modifica la energía total (cinética más potencial) de la partícula. Como el trabajo de la fuerza de rozamiento es negativo y la energía cinética E_k no cambia (velocidad constante), concluimos que la energía potencial final E_pB es menor que la energía potencia inicial E_pA.
En la página titulada "movimiento de un cuerpo en el seno de un fluido ideal", estudiaremos la dinámica del cuerpo y aplicaremos el principio de conservación de la energía.

Energía potencial de un cuerpo parcialmente sumergido

En el apartado anterior, estudiamos la energía potencial de un cuerpo totalmente sumergido en un fluido (un globo de helio en la atmósfera). Ahora vamos a suponer un bloque cilíndrico que se sitúa sobre la superficie de un fluido (por ejemplo agua).
Pueden ocurrir dos casos:

• Que el bloque se sumerja parcialmente si la densidad del cuerpo sólido es menor que la densidad del fluido, r_s< r_f.
• Que el cuerpo se sumerja totalmente si r_s³ r_f.

Cuando el cuerpo está parcialmente sumergido, sobre el cuerpo actúan dos fuerzas el peso mg=r_sSh·g que es constante y el empuje r_fSx·g que no es constante. Su resultante es
F=(-r_sShg+r_fSxg)j.
Donde S el área de la base del bloque, h la altura del bloque y x la parte del bloque que está sumergida en el fluido.
Tenemos una situación análoga a la de un cuerpo que se coloca sobre un muelle elástico en posición vertical. La energía potencial gravitatoria mgy del cuerpo disminuye, la energía potencial elástica del muelle kx²/2 aumenta, la suma de ambas alcanza un mínimo en la posición de equilibrio, cuando se cumple –mg+kx=0, cuando el peso se iguala a la fuerza que ejerce el muelle.

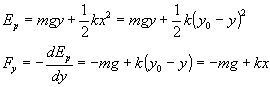
El mínimo de E_p se obtiene cuando la derivada de E_p respecto de y es cero, es decir en la posición de equilibrio.

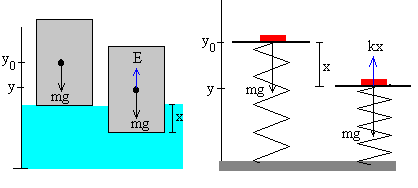
La energía potencial del cuerpo parcialmente sumergido será, de forma análoga

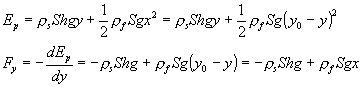
El mínimo de E_p se obtiene cuando la derivada de E_p respecto de y es cero, es decir, en la posición de equilibrio, cuando el peso se iguale al empuje. -r_sShg+r_fSxg=0

El bloque permanece sumergido una longitud x. En esta fórmula, se ha designado r como la densidad relativa del sólido (respecto del fluido) es decir, la densidad del sólido tomando la densidad del fluido como la unidad.

Fuerzas sobre el bloque

1. Cuando r <1 o bien r_s< r_f, el cuerpo permanece parcialmente sumergido en la situación de equilibrio.

2. Cuando r >1 o bien r_s> r_f, el peso es siempre mayor que el empuje, la fuerza neta que actúa sobre el bloque es

F_y=-r_sShg+r_fShg<0.

No existe por tanto, posición de equilibrio, el bloque cae hasta que llega al fondo del recipiente que supondremos muy grande.

3. Cuando r =1 o bien r_s= r_f, El peso es mayor que el empuje mientras el bloque está parcialmente sumergido (x<h).

F_y=-r Shg+r Sxg<0.

La fuerza neta que actúa sobre el bloque cuando está completamente sumergido (x³ h) es cero, y cualquier posición del bloque, completamente sumergido en el seno del fluido, es de equilibrio.

Curvas de energía potencial

1. La energía potencial correspondiente a la fuerza conservativa peso es

E_g= r_sShgy

2. La energía potencial correspondiente a la fuerza de empuje tiene dos partes

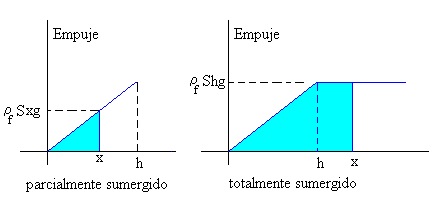
• Mientras el cuerpo está parcialmente sumergido (x<h)

Que corresponde al área del triángulo de la figura de la izquierda.

• Cuando el cuerpo está totalmente sumergido (x³ h)

Que corresponde a la suma del área de un triángulo de base h, y la de un rectángulo de base x-h.

3. La energía potencial total es la suma de las dos contribuciones

E_p=E_g+E_f

Cuando la densidad del sólido es igual a la del fluido r_s= r_f, la energía potencial total E_p es constante e independiente de x (o de y) para x³ h como puede comprobarse fácilmente.

Ejemplos
Una bola de acero de 5 cm de radio se sumerge en agua, calcula el empuje que sufre y la fuerza resultante. Datos: Densidad del acero 7,9 g/cm³
El empuje viene dado por E = d_agua · V_sumergido · g   la densidad del agua se da por conocida (1000 kg/m³), nos queda calcular el volumen sumergido, en este caso es el de la bola. Utilizando el volumen de una esfera:           V = 4/3 p R³ = 4/3 p 0,05³ = 5,236 · 10^-4 m³    por tanto el empuje quedará:
E = d_agua·V_sumergido·g  = 1000 · 5,236 · 10^-4 · 9,8 = 5,131 N
Sobre la bola actúa el empuje hacia arriba y su propio peso hacia abajo, la fuerza resultante será la resta de ambas. El empuje ya lo tenemos, calculamos ahora el peso P = m · g, nos hace falta previamente la masa de la bola, ésta se calcula con su densidad y el volumen (la densidad del acero debe estar en S.I.).
d_acero = 7,9 g/cm³ = 7900 kg/m³         m = d_acero · V = 7900 · 5,234 · 10^-4 = 4,135 kg
P = m · g = 4,135 · 9,8 = 40,52 N
Como vemos el peso es mucho mayor que el empuje, la fuerza resultante será P - E = 35,39 N hacia abajo y la bola se irá al fondo.

Un cubo de madera de 10 cm de arista se sumerge en agua, calcula la fuerza resultante sobre el bloque y el porcentaje que permanecerá emergido una vez esté a flote. Datos: densidad de la madera 700 kg/m³
Este ejercicio es muy similar al anterior, el cuerpo es ahora un cubo de volumen V = lado³ = 0,1³ = 0,001 m³ por tanto el empuje será:
E = d_agua·V_sumergido·g  = 1000 · 0,001 · 9,8 = 9,8 N
La masa del bloque será:
m = d_madera · V = 700 · 0,001 = 0,7 kg
y su peso:
P = m · g = 0,7 · 9,8 = 6,86 N
Vemos que el empuje es mayor que el peso, la fuerza resultante es de 2,94 N hacia arriba lo que hace que el cuerpo suba a flote.
Una vez a flote parte del cuerpo emergerá y no el volumen sumergido disminuirá, con lo cual también lo hace el empuje. El bloque quedará en equilibrio a flote cuando el empuje sea igual al peso y no actúe resultante sobre él, calculemos cuánto volumen permanece sumergido cuando esté a flote.
A flote  E = P            d_agua·V_sumergido·g = Peso      1000 · V_sumergido · 9,8 = 6,86
Despejando V_sumergido =  7 · 10^-4 m³ la diferencia de este volumen bajo el agua y el volumen total del bloque será la parte emergida   V_emergido = 0,001 - 7 · 10^-4 = 3 · 10^-4 m³ emergidos.
El porcentaje de bloque emergido será   3 · 10^-4 /0,001 · 100 = 30 %

Se desea calcular la densidad de una pieza metálica, para ello se pesa en el aire dando un peso de 19 N y a continuación se pesa sumergida en agua dando un peso aparente de 17 N. calcula la densidad del metal.
Si en el agua pesa 2 N menos que fuera es que el empuje vale 2 N, utilizando la fórmula del empuje podemos sacar el volumen sumergido, es decir, el volumen de la pieza.
E = d_agua·V_sumergido·g            2 = 1000 · V · 9,8            V = 2,041 · 10^-4 m³
Sabiendo el peso real de la pieza sacamos su masa   m = P/g = 19/9,8 = 1,939 kg.
Ya sabemos el volumen de la pieza y su masa, por tanto su densidad será:
d = m/V = 1,939/2,041 · 10^-4 = 9499 kg/m³
Ejercicios
1. Un objeto de 5 kg se mete en el agua y se hunde siendo su peso aparente en ella de 30 N, calcula el empuje, su volumen y su densidad.
2. Una pieza de 50 g y un volumen de 25 mL, pesa sumergida en un líquido 0,2 N, calcula la densidad del líquido.
3. Calcula el volumen que se encuentra sumergido en un barco de 10000 toneladas si la densidad del agua del mar es 1030 kg/m³






Soluciones:
1.  19 N; 1,939 · 10^-3 m³; 2579 kg/m³
2.  1183 kg/m³
3.  9709 m³

Ejemplos de ejercicios

Densidad o masa específica 

Densidad de fluidos: cantidad de masa por volumen.

La densidad es la cantidad de masa por unidad de volumen. Se denomina con la letra ρ. En el sistema internacional se mide en kilogramos / metro cúbico.

Cuando se trata de una sustancia homogénea, la expresión para su cálculo es:

Donde

ρ: densidad de la sustancia, Kg/m 3

m: masa de la sustancia, Kg

V: volumen de la sustancia, m 3

en consecuencia la unidad de densidad en el Sistema Internacional será kg/m 3 pero es usual especificar densidades en g/cm 3 , existiendo la equivalencia

1g cm 3 = 1.000 kg/ m 3 .

La densidad de una sustancia varía con la temperatura y la presión; al resolver cualquier problema debe considerarse la temperatura y la presión a la que se encuentra el fluido. 

Peso específico

Presión hidrostática.

El peso específico de un fluido se calcula como su peso por unidad de volumen (o su densidad por g).

En el sistema internacional se mide en Newton / metro cúbico.

 


Presión hidrostática

En general, podemos decir que la presión se define como fuerza sobre unidad de superficie, o bien que la presión es la magnitud que indica cómo se distribuye la fuerza sobre la superficie en la cual está aplicada.

Si una superficie se coloca en contacto con un fluido en equilibrio (en reposo) el fluido, gas o líquido, ejerce fuerzas normales sobre la superficie.

Entonces, presión hidrostática, en mecánica, es la fuerza por unidad de superficie que ejerce un líquido o un gas perpendicularmente a dicha superficie.

Si la fuerza total (F) está distribuida en forma uniforme sobre el total de un área horizontal (A), la presión (P) en cualquier punto de esa área será

P: presión ejercida sobre la superficie, N/m 2

F: fuerza perpendicular a la superficie, N

A: área de la superficie donde se aplica la fuerza, m 2

Mismo nivel, misma presión.

Ahora bien, si tenemos dos recipientes de igual base conteniendo el mismo líquido (figura a la izquierda) , veremos que el nivel del líquido es el mismo en los dos recipientes y la presión ejercida sobre la base es la misma.

Presión solo sobre la base.

Eso significa que:

La presión es independiente del tamaño de la sección de la columna: depende sólo de su altura (nivel del líquido) y de la naturaleza del líquido (peso específico).

Esto se explica porque la base sostiene sólo al líquido que está por encima de ella, como se grafica con las líneas punteadas en la figura a la derecha.

La pregunta que surge naturalmente es: ¿Qué sostiene al líquido restante?

Y la respuesta es: Las paredes del recipiente. El peso de ese líquido tiene una componente aplicada a las paredes inclinadas.

La presión se ejerce solo sobre la base y la altura o nivel al cual llega el líquido indica el equilibrio con la presión atmosférica.

Ver: PSU: Física; Pregunta 13_2005(2)

Presión y profundidad

La presión en un fluido en equilibrio aumenta con la profundidad, de modo que las presiones serán uniformes sólo en superficies planas horizontales en el fluido.

Por ejemplo, si hacemos mediciones de presión en algún fluido a ciertas profundidades la fórmula adecuada es

Es decir, la presión ejercida por el fluido en un punto situado a una profundidad h de la superficie es igual al producto de la densidad d del fluido, por la profundiad h y por la aceleración de la gravedad.

Si consideramos que la densidad del fluido permanece constante, la presión, del fluido dependería únicamente de la profundidad. Pero no olvidemos que hay fluidos como el aire o el agua del mar, cuyas densidades no son constantes y tendríamos que calcular la presión en su interior de otra manera.

Unidad de Presión

En el sistema internacional la unidad es el Pascal (Pa) y equivale a Newton sobre metro cuadrado.

 

La presión suele medirse en atmósferas (atm); la atmósfera se define como 101.325 Pa, y equivale a 760 mm de mercurio o 14,70 lbf/pulg 2 (denominada psi).

La tabla siguiente define otras unidades y se dan algunas equivalencias.

Unidad	Símbolo	Equivalencia
bar	bar	1,0 × 10 5 Pa
atmósfera	atm	101.325 Pa  1,01325 bar  1013,25 mbar
mm de mercurio	mmHg	133.322 Pa
Torr	torr	133.322 Pa
lbf/pulg 2	psi	0,0680 atm
kgf/cm 2		0,9678 atm
	atm	760,0 mmHg
	psi	6.894, 75 Pa

Medidores de presión

Manómetro común.

La mayoría de los medidores de presión, o manómetros , miden la diferencia entre la presión de un fluido y la presión atmosférica local.

Para pequeñas diferencias de presión se emplea un manómetro que consiste en un tubo en forma de U con un extremo conectado al recipiente que contiene el fluido y el otro extremo abierto a la atmósfera.

El tubo contiene un líquido, como agua, aceite o mercurio, y la diferencia entre los niveles del líquido en ambas ramas indica la diferencia entre la presión del recipiente y la presión atmosférica local.

Para diferencias de presión mayores se utiliza el manómetro de Bourdon , llamado así en honor al inventor francés Eugène Bourdon. Este manómetro está formado por un tubo hueco de sección ovalada curvado en forma de gancho.

Los manómetros empleados para registrar fluctuaciones rápidas de presión suelen utilizar sensores piezoeléctricos o electrostáticos que proporcionan una respuesta instantánea.

Como la mayoría de los manómetros miden la diferencia entre la presión del fluido y la presión atmosférica local, hay que sumar ésta última al valor indicado por el manómetro para hallar la presión absoluta. Una lectura negativa del manómetro corresponde a un vacío parcial. 

Ejemplos de ejercicios

Ejemplos de ejercicios:

1.- 0.5 kg de alcohol etílico ocupan un volumen de 0.633 cm³. Calcular su densidad y peso específico.

Datos:

M = 0.5kg               P = m/V                                  Pe = pg

V = 0.633 cm³        P = 0.5 kg/ 6.33*10^-7 m³      Pe = (789889.41 kg/ m³)(9.81 m/s²)

= 6.33*10^-7 m³     P = 789889.41 kg/ m³              Pe = 7748815.11 nw/ m³


2.- ¿Cuántos m3 ocuparán 1000 kg de aceite de linaza, si este tiene una densidad de 940 kg/ m³?

Datos:

M = 1000kg            P = m/V

P = 940 kg/m³        V = m / p

V = ?                       V= 1000kg / 940 kg/m³

                               V = 1.063 m³


3.- Determine la masa de un cubo de 5 cm de arista si el material con que está construido es de cobre.

Datos:

V = 5cm = 0.05 m             P = m/V

V = 1.25x10^-4                  M = pv

P = 8960kg/m³                 M = (8960kg/m³)(1.25x10^-4)

M = ?                                M = 1.12 kg/m³


4.- Un objeto tiene una masa de 128.5 kg y un volumen de 3.25 m³
a) ¿Cuál es su densidad?
b) ¿Cuál es su peso específico?

Datos:

M = 128.5kg             P = m/v                            Pe = pg

V = 3.25m³              P = 128.5kg / 3.25 m³      Pe = (39.53kg/m³)(9.81m/s²)

P = ?                          P = 39.53 kg/m³               Pe= 387.78 Nw/m³

Pe = ?


5.- Un objeto tiene una masa de 2190 kg.
a) ¿Cuál es el peso del objeto?
b) Si el volumen que ocupó es de 0.75 m³, ¿Cuál es su peso específico?

Datos:

M = 2190kg               W = mg                                    Pe = w/v

W = ?                         W= (2190kg)(9.81m/s²)        Pe = 21483.9Nw/0.7m³

Pe = ?                         W= 21483.9 Nw                   Pe = 28045.2 Nw/m³

V = 0.75m³

HIDROSTATICA

HIDROSTATICA E HIDRODINAMICA

lunes, 8 de octubre de 2012

HIDROSTATICA

1.- CONCEPTO:

La Hidrostática es la parte de la física que estudia los fluidos líquidos en reposo. Entendemos por fluido cualquier sustancia con capacidad para fluir, como es el caso de los líquidos y los gases.  Éstos se caracterizan por carecer de forma propia y por lo tanto, adoptar la del recipiente que los contiene.  Por otra parte, los líquidos (difícilmente compresibles) poseen volumen propio mientras que los gases (compresibles), ocupan la totalidad del volumen del recipiente que los contiene.

2.- FUERZA Y PRESIÓN

En la primera unidad vimos el concepto de fuerza, una magnitud vectorial que representa la acción sobre un cuerpo. La presión es una magnitud escalar, y se define como la fuerza que actúa sobre un cuerpo por unidad de área. Así por ejemplo, la presión atmosférica es la fuerza que ejerce el aire que nos rodea sobre la superficie terrestre.

                                   P = F / S

La presión que ejerce un fluido sobre las paredes del recipiente que lo contiene es siempre perpendicular a dicha superficie. 

3.- UNIDADES: 

veamos cuales son las unidades de presión en los tres sistemas métricos.

A la unidad del sistema C.G.S. ( dina / cm2 ) se la denomina baria y a la unidad del M.K.S. (N/m2) se la denomina Pascal.  En el apéndice, al final del capítulo,  se dan otras unidades de presión, con las respectivas equivalencias entre ellas. Volveremos sobre este tema en la unidad III al hablar de presión atmosférica.

4.- EQUIVALENCIAS ENTRE LOS TRES SISTEMAS: 

 

La siguiente igualdad establece la equivalencia entre las unidades de los tres sistemas vistos:

EJERCICIO A: Sobre un clavo de cuya cabeza tiene una superficie de 7 mm2 se ejerce una fuerza con un martillo de 150 N. Calcular la presión que ejerce la punta del clavo sobre una madera, sabiendo que la superficie de dicha punta es de 1 mm2. Expresar dicha presión en los tres sistemas de unidades.

A) PRESIÓN EN UN PUNTO DE UNA MASA LÍQUIDA

Se define como la fuerza que actúa por unidad de área, normalmente (perpendicularmente) a un elemento de superficie situado en dicho punto.

• TEOREMA GENERAL DE LA HIDROSTÁTICA

Podemos ahora enunciar el Principio General de la Hidrostática de la siguiente manera:

En la figura siguiente, Pa y Pb son las presiones en dos puntos diferentes de la masa líquida, r es el peso específico del líquido y h la distancia vertical entre ambos puntos:

 

B) PRESIÓN SOBRE PAREDES Y FONDO EN RECIPIENTES

Las presiones ejercidas por un líquido sobre las paredes y el fondo del recipiente que lo contiene, son siempre perpendiculares a la superficie. Esto lo vamos a comprobar en el primer trabajo práctico. 

En la figura que sigue, la presión en el fondo del recipiente (Pb) es la suma entre la presión ejercida sobre la superficie del líquido (presión atmosférica) y el producto del peso específico por la altura de éste:

EJERCICIO B: Calcular la presión que soporta el fondo de un tanque con glicerina de 1.65 m de altura si la presión atmosférica es 1013.25 HPa. ¿Cuál será la presión con la que sale el líquido si se perfora un orificio a 40 cm del fondo del tanque?

5.- PARADOJA   HIDROSTÁTICA

Volviendo al ejemplo de la pileta, vimos que al sumergirnos, aumenta la presión sobre nuestro cuerpo a medida que descendemos. Ahora nos preguntamos ¿Tiene algo que ver la forma de la pileta con la presión que soportamos?

La presión ejercida en el fondo del recipiente depende del peso específico y de la altura del líquido siendo independiente de la forma del recipiente y de la cantidad de líquido contenido en él.

 

6.- PRESIÓN DE ABAJO HACIA ARRIBA

            En el interior de un líquido, la presión se ejerce en todas direcciones en cada punto. Se puede demostrar experimentalmente que la presión hacia arriba es igual a la presión hacia abajo, como lo muestra el siguiente dibujo:

7.- VASOS COMUNICANTES

Si colocamos varios recipientes con formas diferentes conectados entre sí por su parte inferior, tendremos entonces un sistema de vasos comunicantes.

Suponiendo que todos los recipientes están abiertos en su parte superior y volcamos agua dentro de ellos, ¿qué esperas que ocurra con el nivel del líquido en todos ellos?

En los V.C. con un solo líquido, éste alcanza el mismo nivel en todos los recipientes pues la superficie está sometida a la misma presión (atmosférica) y todos los puntos que están a igual nivel tienen la misma presión:

8.- PO : PRESIÓN ATMOSFÉRICA

En los V.C. con dos líquidos distintos, inmiscibles y de diferente densidad, éstos alcanzan distintos niveles.

9.- PRINCIPIO DE PASCAL

            El físico, matemático, filósofo y escritor francés, Blas Pascal (1623 - 1662) enunció el siguiente principio:

"La presión ejercida sobre la superficie libre de un líquido en equilibrio se transmite íntegramente y en todo sentido a todos los puntos de la masa líquida”.

En la figura anterior se verifica el principio de Pascal, en la cual PA y PB son las presiones ejercidas en los puntos A y B respectivamente antes de aplicar la fuerza F y P'A y P'B son las presiones luego de aplicar dicha fuerza. La presión P es la generada por la aplicación de la fuerza F sobre la superficie S en A.

Para comprobar este principio se utiliza un dispositivo como el de la figura siguiente:

Se observa experimentalmente que al aplicar una presión sobre el pistón del tubo central, el nivel de líquido asciende valores iguales en todos los tubos laterales.

EJERCICIO C: Calcular la presión ejercida en el fondo de un tanque de 25 m de altura con petróleo  si efectuamos sobre la superficie de éste una presión de 150 N/cm2. ¿Cuál sería la presión si el tanque estuviera sometido a la presión atmosférica normal?

10.- PRENSA HIDRÁULICA

            Es un dispositivo para obtener fuerza de compresión mayor, basada en el principio de Pascal. Si sobre un líquido encerrado en un recipiente, aplicamos una fuerza F1 sobre una superficie S1, podemos obtener una fuerza F2 mayor que F1 en otro émbolo de sección S2 mayor que S1:

11.- DENSIDAD Y PESO ESPECÍFICO

            Se define densidad al cociente entre la masa de un cuerpo homogéneo y su volumen.  El peso específico, en cambio, es el cociente entre el peso del cuerpo  (P = m.g) y el volumen.

            Las unidades se obtienen de dividir las unidades de masa o peso por las de volumen:

            Densidad: g/cm3, kg/m3                   Peso específico: dina/cm3, N/m3, etc. 

            Un método rápido para determinar el peso específico de un cuerpo consiste en suspender el cuerpo de un dinamómetro (determinando su peso en el aire P) y luego sumergirlo en un recipiente con agua, siendo en este caso su peso P'.

A) TABLA DE PESOS ESPECÍFICOS DE SÓLIDOS Y LÍQUIDOS

            Sustancia                 Pe (g/cm3)               Sustancia                 Pe (g/cm3)  

            Aceite de Oliva      0,92                           Estaño                             7,30    

            Agua                         1,00                            Granito                           2,70    

            Agua de mar           1,02                            Glicerina                       1.26    

            Alcohol etílico         0,79                            Hielo                                0,92    

            Aluminio                    2,73                            Hierro                              7,86    

Ámbar                       1,01                            Leche                             1,08    

            Azúcar                      1,60                            Mercurio                        13,6    

            Azufre                        2,10                            Nafta                             0,70    

            Caucho                    0,90                            Níquel                             8,60    

            Celuloide                  1,40                            Oro                                 19,29  

            Cinc                           7,15                            Petróleo                         0,75    

            Cloruro de Sodio     2,10                            Plata                             10,51  

            Cobre                        8,50                            Platino                          21,43  

            Corcho                     0,22                            Plomo                             11,33  

            Cuarzo                      2,65                            Uranio                             18,98  

12.- PESO ESPECÍFICO DE UN MEZCLA:

            Veamos como calcular el peso específico de una mezcla sólida o líquida:

Pe _mezcla= 1/(S x_mi/Pe_i ) =  S x_vi . Pe_i )

Donde S significa sumatoria, X_mi fracción en masa del componente i y X_vi fracción en volumen del componente i.

13.- EJERCICIOS

• Si deseas ampliar tus conocimientos resulve los siguientes ejercicios:

1.- Calcular la presión ejercida  en lib/pulg² por el agua sobre la base de un tanque cilíndrico de 158 cm de diámetro y 3.000 l de capacidad.                                                                       

2.- El pistón de un elevador hidráulico para automóviles tiene 30 cm de diámetro. ¿ Qué presión en libras/pulgada2 deberá ejercer para levantar un automóvil que pesa 1500 kgf?

3.- Calcular la presión que soporta una plataforma para sostener un tanque rectangular de agua de 12.000 l de capacidad sabiendo que el nivel del líquido en el tanque alcanza una altura máxima de 2 m y el peso del tanque vacío es de 1 ton.

4.- ¿Cuál es la presión que soporta un buzo sumergido a 16 m de la superficie sabiendo que a 2 metros de profundidad la presión es de 1257,87 g/cm2 y el peso específico del agua es de 1,12 g/cm3.    ¿Cuál es la presión atmosférica en el lugar?

5.- Un cilindro de Al (r = 2,7 g/cm3) de 3 cm de diámetro y 5 cm de altura se lo sumerge en glicerina (r = 1.26 g/cm3) y luego en mercurio (r =13,6 g/cm3). Determinar en cuál de los dos líquidos está totalmente sumergido y cuál será la altura que tendrá el nivel del líquido, medida sobre la altura del cilindro, para el caso en que flota.                                                                  

6.- Un paralelepípedo construido en bronce ( r = 8.6 g/cm3 ) posee una altura de 7 cm. ¿Qué porcentaje del paralelepípedo se sumergirá en un recipiente conteniendo mercurio? ¿ Qué ocurre si la altura del paralelepípedo es el doble? ¿De qué depende la fracción sumergida?

                                                                                                            

7.- Se desea construir una prensa hidráulica que permita obtener una fuerza de compresión de 650 N y se dispone de un émbolo de 100 cm2 de sección y una fuerza máxima de 30 Kg. ¿Cuál deberá ser la sección del otro émbolo? ¿ Podría utilizarse un émbolo de 45 cm2 de sección?

                                                                                       

8.- Se desea determinar simultáneamente los pesos específicos del plomo y el alcohol. Para ello se suspende una pesa de plomo de 2 kg. de un dinamómetro y se lo sumerge dentro de una probeta de un litro conteniendo 800 cm3 de alcohol. Cuando la pesa está totalmente sumergida, el nivel de líquido en la probeta es de 977 cm3 y el dinamómetro marca 1,857 kg.

                                                                               

9.- Se desea saber de qué material está hecha una esfera maciza de 2 cm de radio para lo cual se la coloca dentro de un recipiente de 3,93 cm de radio con mercurio observándose que el nivel de éste asciende 4 mm sin que se sumerja totalmente. A partir de los datos del apéndice determine el material de la esfera y su peso.                                            

  

10.- Con el objeto de determinar la composición de una aleación de cobre y estaño de 4 kg, se la suspende de un dinamómetro y al sumergirlo en agua éste marca 3,5 kg. Sabiendo que la densidad del cobre es 8.93 g/ml y la del estaño es 5.75 g/ml, calcular la composición centesimal de la aleación.                                                                                                        

11.- Una boya cilíndrica de 90 cm de diámetro y 1.500 kg flota verticalmente en el mar (r= 1.08 g/cm3). Calcular cuánto se hundirá si dos personas de 80 kg c/u se suben a ella.          

12.- ¿Qué porcentaje de una esfera hueca de alumnio (Pe: 2.73 g/cm3) se sumergirá en un recipiente con agua, si el espesor de la esfera es de 8 mm y su diámetro es de 15 cm?