Introducción
Hagámonos una pregunta: ¿Qué cosas se mueven? Un automóvil que viaja hacia la costa; una hoja que, agitada por el viento, cae de un árbol; una pelota que es pateada por un futbolista; un atleta que corre tras una meta; un electrón que vibra en su entorno; la Tierra alrededor del Sol.
 |
| Todo se mueve. |
Quizás deberíamos preguntarnos ¿hay algo que no se mueva?
Como la respuesta parece obvia (“todo se mueve”) aboquémonos a averiguar ¿qué es movimiento?
Si nos referimos a un objeto que se mueve, diríamos que el objeto tiene movimiento si cambia de posición a través del tiempo.
Entonces, se define el movimiento como un cambio de posición de un cuerpo con respecto a otro cuerpo (donde se sitúa un observador), durante un espacio de tiempo.
El carácter relativo del movimiento
¿Han escuchado hablar de relatividad? Relatividad es un concepto muy utilizado cuando se intenta describir un movimiento.
De acuerdo con la anterior definición, para estudiar un movimiento es preciso fijar previamente la posición del observador que contempla dicho movimiento.
En física hablar de un observador equivale a situarlo fijo con respecto al objeto o conjunto de objetos que definen el sistema de referencia. Es posible que un mismo cuerpo esté en reposo para un observador —o visto desde un sistema de referencia determinado— y en movimiento para otro.
De hecho, los movimientos son relativos. Relativos a un sistema de referencia.
 |
| El metro se mueve con respecto a la estación. |
Y un sistema de referencia es algo que suponemos en reposo. Respecto al cual describimos los movimientos.
Así, un pasajero sentado en el interior de un avión que despega estará en reposo respecto del propio avión y en movimiento respecto de la pista de aterrizaje.
Otro ejemplo: una estación de metro es el sistema de referencia para los vagones que se mueven dentro de ella. Si hablamos de un automóvil que se mueve, en realidad estamos usando — sin nombrarlo explícitamente— un sistema de referencia. En este caso sería el suelo, la porción de la superficie de la tierra en donde se desplaza el automóvil. Mientras una roca permanece en su lugar en el suelo, el automóvil va ocupando sucesivamente distintas posiciones respecto del suelo.
El estado de reposo o de movimiento de un cuerpo no es, por tanto,absoluto o independiente de la situación del observador, sino relativo; es decir, depende del sistema de referencia desde el que se observe.
Pero veamos lo que sucede a los ocupantes del automóvil de nuestro ejemplo.
Vistas desde fuera del automóvil, las personas que van en su interior también se mueven junto al automóvil. Llevan la misma rapidez, la misma velocidad del automóvil.
Vistas desde dentro del automóvil, las personas están en reposo una respecto a la otra. Podríamos darnos cuenta que una no se mueve respecto a otra, permanecen siempre a la misma distancia entre sí. A lo más habrá movimientos pequeños, limitados por el tamaño del interior del automóvil.
Entonces, una persona que va en el automóvil se mueve respecto al suelo con la misma rapidez y velocidad que el automóvil; sin embargo, respecto a otra persona u objeto que está en el interior del mismo, esa persona no tendría movimiento.
 |
| Los ocupantes del automóvi ¿se mueven o están en reposo? |
Tomando en cuenta lo anterior, habrá que referirse a un sistema de referencia cuando queramos hablar de que algo se mueve. Habrá que decir, por ejemplo, que “tal cosa se mueve respecto a...”
Ahora bien, en el lenguaje común, cuando no hacemos mención a un sistema de referencia, el sistema de referencia utilizado será la superficie de la Tierra. Es decir, cuando decimos que un automóvil viaja a 60 kilómetros por hora, es respecto a la superficie de la Tierra que el automóvil tiene esa rapidez. La superficie de la Tierra la estamos considerando en reposo.
Estudio de los movimientos
La observación y el estudio de los movimientos se conoce desde tiempos remotos. Los griegos decían “Ignorar el movimiento es ignorar la naturaleza”, y con ello que reflejaban la importancia capital que se le otorgaba al tema.
Luego, científicos y filósofos medievales observaron los movimientos de los cuerpos y especularon sobre sus características. Los propios artilleros de la época manejaron de una forma práctica el tiro de proyectiles de modo que supieron inclinar convenientemente el cañón para conseguir el máximo alcance de la bala. Sin embargo, el estudio propiamente científico del movimiento se inicia conGalileo Galilei. A él se debe una buena parte de los conceptos que se refieren al movimiento.
El concepto de cinemática
El concepto de cinemática
Es posible estudiar el movimiento de dos maneras:
a) describiéndolo, a partir de ciertas magnitudes físicas, a saber: posición, velocidad y aceleración (cinemática);
b) analizando las causas que originan dicho movimiento (dinámica).
En el primer caso se estudia cómo se mueve un cuerpo, mientras que en el segundo se considera el por qué se mueve.
La cinemática, entonces, es la parte de la física que estudia cómo se mueven los cuerpos sin pretender explicar las causas que originan dichos movimientos.
La dinámica es la rama de la física que se ocupa del movimiento de los objetos y de su respuesta a las fuerzas.
El tiempo y el espacio
 |
Para hablar de movimiento es imprescindible referirse a dos magnitudes elementales de la física como son el espacio y el tiempo.
Íntimamente relacionados, el tiempo (t) permite ordenar los sucesos físicos en una escala que distingue entre pasado, presente y futuro, mientras que el espacio (s) puede verse como un medio abstracto en el que se desplazan los cuerpos. Se describe normalmente mediante tres coordenadas que corresponden a la altura, la anchura y la profundidad.
Ahora bien, al referirnos al movimiento, que sabemos se realiza en un espacio y en un tiempo determinados, es preciso tener en cuenta, además, que éste posee varias características (o condiciones) que lo convierten en tal. Si falta alguna de ellas, el movimiento no se puede realizar.
Estas características, condiciones o conceptos involucrados en el movimiento son:
Posición, desplazamiento, trayectoria, velocidad, aceleración y deceleración.
Posición
La posición x del móvil se puede relacionar con el tiempo t mediante una función x = f(t).
Desplazamiento
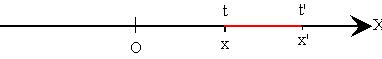
Supongamos ahora que en el tiempo t, el móvil se encuentra en posición x, más tarde, en el instante t' el móvil se encontrará en la posición x'. Decimos que móvil se ha desplazado Δx = x' – x en el intervalo de tiempo Δt = t' – t, medido desde el instante t al instante t'.
Trayectoria
Para simplificar el estudio del movimiento, representaremos a los cuerpos móviles por puntos geométricos, olvidándonos, por el momento, de su forma y tamaño.
Se llama trayectoria a la línea que describe el punto que representa al cuerpo en movimiento, conforme va ocupando posiciones sucesivas con el transcurso del tiempo.
Una trayectoria puede adoptar diversas formas: rectilínea, curva, parabólica, mixta, etc.
La estela que deja en el cielo un avión a reacción o los rieles de una línea de ferrocarril son representaciones aproximadas de esa línea imaginaria que se denomina trayectoria.
 |
| Trayectoria de una pelota de golf. |
Según sea la forma de su trayectoria los movimientos se clasifican en rectilíneos ycurvilíneos (o circulares).
Un automóvil que recorra una calle recta describe un movimiento rectilíneo, mientras que cuando tome una curva o dé una vuelta a una plaza circular, describirá un movimiento curvilíneo.
Según esta clasificación podemos encontrar:
El movimiento rectilíneo uniforme lo tiene un objeto cuando cambia de posición en el tiempo (movimiento) en una trayectoria que es una línea recta (rectilíneo) y con velocidad constante (uniforme).
En la naturaleza existen movimientos que se aproximan bastante al movimiento rectilíneo. Buenos ejemplos son: un hombre o animal caminando regularmente, el movimiento de una gota de agua al final de su caída en un día sin viento, el movimiento de la luz en un medio determinado (homogéneo en cuanto a su densidad), el movimiento del sonido en un medio determinado (homogéneo en cuanto a su densidad).
Otros ejemplos, no naturales, podrían ser: el de un automóvil en una carretera recta, aunque en este caso el movimiento rectilíneo uniforme se presenta en tramos. Es muy difícil que —estrictamente hablando— el automóvil se mueva sin modificar en absolutamente nada su velocidad.
A pesar de que el movimiento rectilíneo uniforme no es lo más común que existe, su estudio es muy útil pues hay muchos movimientos que pueden aproximarse a este tipo.
La velocidad
La descripción de un movimiento supone el conocer algo más que su trayectoria y su desplazamiento. Una característica que añade una información importante sobre el movimiento es la rapidez. En general, cuando algo cambia con el tiempo se emplea el término de rapidez para describir su ritmo de variación temporal. En cinemática la rapidez con la que se produce un movimiento se denominavelocidad y se define como el espacio que recorre el móvil sobre la trayectoria en la unidad de tiempo.
Velocidad constante
 |
| Velocidad constante, sólo en ciertos tramos. |
Decir que un cuerpo se mueve con velocidad constante es lo mismo que decir que la rapidez de su movimiento no varía; es decir, que va recorriendo la trayectoria y ganando espacio siempre al mismo ritmo.
Los movimientos de los trenes o los de los coches en una autopista se aproximan bastante en algunos tramos a movimientos de velocidad constante. En dos intervalos de tiempo cualesquiera de igual duración el cuerpo cubrirá la misma distancia.
El móvil recorre, por tanto, espacios iguales en tiempos iguales, lo cual significa que cuando la velocidad es constante el espacio s que recorre el cuerpo móvil sobre la trayectoria y el tiempo t que emplea en recorrerlo son magnitudes directamente proporcionales.
La unidad de medida de la velocidad es el cociente entre la unidad de medida de espacio o distancia y la unidad de tiempo. En el Sistema Internacional (SI) es el metro/segundo (m/s) o ms–1. Sin embargo, resulta muy frecuente en la vida diaria la utilización de una unidad práctica de velocidad, el kilómetro/hora (km/h),que no corresponde al SI. La relación entre ambas es la que sigue:
o inversamente
Velocidad media
La prensa diaria publica, de vez en cuando, la velocidad media de circulación en automóvil característica de las grandes ciudades. Si en Santiago, por ejemplo, se cifra en 20 km/h. ello no significa que los coches se desplacen por las calles siempre a esa velocidad.
Tomando como referencia un trayecto de 10 km, el coche puede alcanzar los 60 o incluso los 70 km/h, pero en el trayecto completo ha de frenar y parar a causa de las retenciones, de modo que para cubrir los 10 km del recorrido establecido emplea media hora. La velocidad del coche ha cambiado con el tiempo, pero, en promedio, y a efectos de rapidez el movimiento equivale a otro que se hubiera efectuado a una velocidad constante de 20 km/h.
Velocidad instantánea
 |
| Una escalera mecánica, se mueve a velocidad constante. |
En general, la velocidad con la que se mueve un coche, un avión o una motocicleta, por ejemplo, varía de un instante a otro. Ello queda reflejado en el movimiento de la aguja de sus respectivos velocímetros.
El valor que toma la velocidad en un instante dado recibe el nombre develocidad instantánea.
Aun cuando la noción de instante, al igual que la noción de punto, constituye una abstracción, es posible aproximarse bastante a ella considerándola como un intervalo de tiempo muy pequeño.
Así, la lectura del velocímetro se produce en centésimas de segundos y ese tiempo puede ser tomado en el movimiento de un coche como un instante, ya que durante él la velocidad prácticamente no cambia de magnitud.
En los movimientos ordinarios la velocidad no se mantiene constante, sino que varía con el tiempo. En tales casos es posible definir una nueva magnitud que describa la rapidez con la que se producen tales variaciones de la velocidad. Dicha magnitud se denomina aceleración.
Se define como lo que varía la velocidad en la unidad de tiempo y representa, por tanto, el ritmo de variación de la velocidad con el tiempo.
Una de las características que definen la potencia de un automóvil es su capacidad para ganar velocidad. Por tal motivo, los fabricantes suelen informar de ello al comprador, indicando qué tiempo (en segundos) tarda el modelo en cuestión en alcanzar los 100 km/h partiendo del reposo. Ese tiempo, que no es propiamente una aceleración, está directamente relacionado con ella, puesto que cuanto mayor sea la rapidez con la que el coche gana velocidad, menor será el tiempo que emplea en pasar de 0 a 100 km/h.
Aceleración constante
Un cuerpo que se mueva con aceleración constante irá ganando velocidad con el tiempo de un modo uniforme; es decir, al mismo ritmo. Eso significa que lo que aumenta su velocidad en un intervalo dado de tiempo es igual a lo que aumenta en otro intervalo posterior, siempre y cuando las amplitudes o duraciones de ambos intervalos sean iguales.
En otros términos, el móvil gana velocidad en cantidades iguales si los tiempos son iguales y la velocidad resulta, en tales casos, directamente proporcional al tiempo.
Del mismo modo que para definir la velocidad es necesario poner la atención en la relación entre espacio y tiempo, para definir la aceleración es preciso pensar sólo en términos de velocidad y tiempo.
Aceleración media
La aceleración media representa lo que por término medio varía la velocidad en cada unidad de tiempo.
Aun cuando la velocidad de un móvil cambie de un modo irregular, o no uniforme, es posible considerar otro movimiento equivalente al anterior, en lo que a la ganancia de velocidad respecta, que aumente su velocidad lo mismo y en el mismo tiempo, pero sólo que a un ritmo constante. La aceleración de ese movimiento equivalente, pero de aceleración constante es, precisamente, la aceleración media.
Aceleración instantánea
 |
| Aumentos o variaciones de velocidad, resultado de aceleraciones. |
Es la aceleración referida a un intervalo de tiempo lo suficientemente pequeño como para poder considerar despreciable la variación de la velocidad del móvil durante él.
Aun cuando los automóviles no disponen de acelerómetro o medidor de aceleración, su fabricación sería relativamente sencilla y permitiría la lectura instantánea de la magnitud aceleración.
Que en un momento dado la columna luminosa de un acelerómetro marcase 7 m/s2 significaría que, de mantenerse constante el ritmo de progresión del movimiento leído para ese instante, el automóvil ganaría velocidad a razón de 7 metros por segundo en cada segundo.
Deceleraciones
Aun cuando las variaciones de velocidad consideradas hasta ahora han sido únicamente aumentos, un móvil puede también disminuir su velocidad con el tiempo. En tales casos, los valores de la velocidad posteriores en el tiempo son menores que los anteriores, por lo que su variación es negativa. Esta aceleración negativa es característica de los movimientos de frenado y recibe el nombre de deceleración.
La deceleración es un tipo particular de aceleración, por lo que ha de considerarse como tal. Sólo el signo menos indica que está asociada a un movimiento cuya velocidad disminuye con el tiempo.
La representación gráfica de un movimiento y de sus características permite extraer una información valiosa sobre dicho movimiento.
La trayectoria es una primera descripción gráfica del movimiento; en ella no se recoge (explícitamente) la variable tiempo, sino que se representan únicamente las posiciones del punto móvil, o, lo que es lo mismo, la relación entre sus coordenadas a lo largo del movimiento. Es, por tanto, una gráfica espacial.
 |
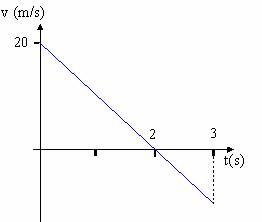| En el diagrama, la velocidad (en m/s) en el eje vertical; el tiempo (en seg.) en el eje horizontal. |
Las gráficas en las que se refleja la variación de diferentes magnitudes con respecto al tiempo son gráficas temporales y por sí mismas proporcionan una buena descripción de las características del movimiento considerado.
En todas ellas el tiempo t se representa en el eje horizontal o de abscisas y la magnitud cinemática elegida —como el espacio s, la velocidad v o la aceleración a— se representa en el eje vertical o de ordenadas.
La variación con respecto al tiempo de cada una de estas magnitudes da lugar a la correspondiente gráfica o diagrama cinemático.
Vectores para la cinemática
Cuando se pretende estudiar un movimiento de la forma más completa posible, es necesario considerar las magnitudes cinemáticas tales como el desplazamiento, la velocidad o la aceleración de modo que recojan los aspectos direccionales del movimiento; es decir, los cambios de orientación del punto móvil en el espacio y sus consecuencias. Para ello se recurre a los vectores, esos elementos matemáticos que permiten describir los aspectos relativos a la dirección y al sentido.
El vector velocidad
La velocidad es la variación de la posición de una partícula en una determinada cantidad de tiempo; es decir, es cuánto varió la posición de la partícula en un lapso de tiempo.
La velocidad es una magnitud vectorial, por tanto tiene un módulo y una dirección. El módulo define el "tamaño" que tiene la velocidad, mientras que la dirección define hacia donde apunta esa velocidad. Por ejemplo, un automóvil puede tener una velocidad de 90 Km/h con una dirección Norte-Sur.
La velocidad suele usarse como sinónimo de rapidez, pero esta última es una magnitud que sólo representa el módulo (medida numérica) de la velocidad.
La velocidad entre los instantes t1 y t2 está definida por
La velocidad (V), como dijimos, es una magnitud vectorial y, por tanto, se representa mediante un vector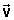 
Los cuatro elementos de este vector son:
 |
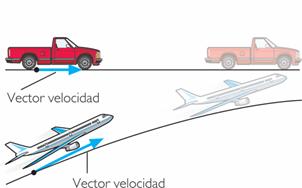| El vector velocidad representa la rapidez con la que cambia la posición del cuerpo en el movimiento cuando se considera ésta como un vector. |
• Punto de aplicación. La posición del punto móvil.
• Dirección. Recta tangente a la trayectoria.
• Sentido. El del movimiento.
• Módulo o intensidad. Es el valor numérico: dado por la fórmula
El vector aceleración
El vector aceleración representa la rapidez con la que el vector velocidad de un cuerpo móvil cambia con el tiempo.
La aceleración se define como la razón entre el cambio de velocidad y el intervalo en el cual ésta ocurre.
Supongamos que en un instante t1 la velocidad del móvil es v1, y en el instante t2 la velocidad del móvil es v2.
Se denomina aceleración entre los instantes t1 y t2 al cociente entre el cambio de velocidad Δv = v2 – v1 y el intervalo de tiempo en el que se ha tardado en efectuar dicho cambio, Δt = t2 – t1.
MOVIMIENTO RECTILINEO
 |
| Movimiento rectilíneo, si sigue una línea recta. |
Los movimientos rectilíneos, que siguen una línea recta, son los movimientos más sencillos. Movimientos más complicados pueden ser estudiados como la composición de movimientos rectilíneos elementales. Tal es el caso, por ejemplo, de los movimientos de proyectiles.
El movimiento rectilíneo puede expresarse o presentarse como
Movimiento rectilíneo uniforme, o como
Este último puede, a su vez, presentarse como de caída libre o de subida vertical.
Movimiento rectilíneo uniforme
El movimiento rectilíneo uniforme (MRU) fue definido, por primera vez, por Galileo en los siguientes términos: "Por movimiento igual o uniforme entiendo aquél en el que los espacios recorridos por un móvil en tiempos iguales, tómense como se tomen, resultan iguales entre sí", o, dicho de otro modo, es un movimiento de velocidad v constante.
El MRU se caracteriza por:
a) Movimiento que se realiza en una sola dirección en el eje horizontal.
b) Velocidad constante; implica magnitud, sentido y dirección inalterables.
c) La magnitud de la velocidad recibe el nombre de rapidez. Este movimiento no presenta aceleración (aceleración = 0).
 |
| Rapidez fantástica. |
Concepto de rapidez y de velocidad
Muy fáciles de confundir, son usados a menudo como equivalentes para referirse a uno u otro.
Pero la rapidez (r) representa un valor numérico, una magnitud; por ejemplo, 30 km/h.
En cambio la velocidad representa un vector que incluye un valor numérico (30 Km/h) y que además posee un sentido y una dirección.
Cuando hablemos de rapidez habrá dos elementos muy importantes que considerar: la distancia (d) y el tiempo (t), íntimamente relacionados.
Así:
Si dos móviles demoran el mismo tiempo en recorrer distancias distintas, tiene mayor rapidez aquel que recorre la mayor de ellas.
Si dos móviles recorren la misma distancia en tiempos distintos, tiene mayor rapidez aquel que lo hace en menor tiempo.
Significado físico de la rapidez
La rapidez se calcula o se expresa en relación a la distancia recorrida en cierta unidad de tiempo y su fórmula general es la siguiente:
 |
Donde
v = rapidez d = distancia o desplazamiento t = tiempo
|
Usamos v para representar la rapidez, la cual es igual al cociente entre la distancia (d) recorrida y el tiempo (t) empleado para hacerlo.
Como corolario, la distancia estará dada por la fórmula:
Según esta, la distancia recorrida por un móvil se obtiene de multiplicar su rapidez por el tiempo empleado.
A su vez, si se quiere calcular el tiempo empleado en recorrer cierta distancia usamos
El tiempo está dado por el cociente entre la distancia recorrida y la rapidez con que se hace.
Ver: PSU: Física; Pregunta 04_2005(2)
 |
| En este ejemplo, el móvil recorre 8 metros cada 2 segundos y se mantiene constante. |
Problemas o ejercicios sobre el movimiento rectilíneo uniforme:
Ejercicio 1
Un automóvil se desplaza con una rapidez de 30 m por segundo, con movimiento rectilíneo uniforme. Calcule la distancia que recorrerá en 12 segundos.
Analicemos los datos que nos dan:
Apliquemos la fórmula conocida:
y reemplacemos con los datos conocidos:
¿Qué hicimos? Para calcular la distancia (d), valor desconocido, multiplicamos la rapidez (v) por el tiempo (t), simplificamos la unidad segundos y nos queda el resultado final en metros recorridos en 12 segundos: 360 metros
Ejercicio 2
 |
El automóvil de la figura se desplaza con movimiento rectilíneo uniforme ¿cuánto demorará en recorrer 258 kilómetros si se mueve con una rapidez de 86 kilómetros por hora?
Analicemos los datos que nos dan:
Apliquemos la fórmula conocida para calcular el tiempo:
y reemplacemos con los datos que tenemos:
¿Qué hicimos? Para calcular el tiempo (t), valor desconocido, dividimos la distancia (d) por la rapidez (v), simplificamos la unidad kilómetros y nos queda el resultado final en horas: 3 horas para recorrer 258 km con una rapidez de 86 km a la hora.
Ejercicio 3
¿Con qué rapidez se desplaza un móvil que recorre 774 metros en 59 segundos?
Analicemos los datos conocidos:
Aplicamos la fórmula conocida para calcular la rapidez:
¿Qué hicimos? Para calcular la rapidez (v), valor desconocido, dividimos la distancia (d) por el tiempo (t), y nos queda el resultado final: la rapidez del móvil para recorrer 774 metros en 59 segundos: 13,11 metros por segundo.
 |
| Un móvil puede ser acelerado. |
Ya vimos que el movimiento rectilíneo puede expresarse o presentarse como
Movimiento rectilíneo uniforme,
o como
Movimiento rectilíneo uniformemente acelerado.
Este último puede, a su vez, presentarse como de caída libre o de subida o tiro vertical.
El movimiento rectilíneo uniformemente aceleradoes un tipo de movimiento frecuente en la naturaleza. Una bola que rueda por un plano inclinado o una piedra que cae en el vacío desde lo alto de un edificio son cuerpos que se mueven ganando velocidad con el tiempo de un modo aproximadamente uniforme; es decir, con una aceleración constante.
Este es el significado del movimiento uniformemente acelerado, el cual “en tiempos iguales, adquiere iguales incrementos de rapidez”.
En este tipo de movimiento sobre la partícula u objeto actúa una fuerza que puede ser externa o interna.
En este movimiento la velocidad es variable, nunca permanece constante; lo que si es constante es la aceleración.
Entenderemos como aceleración la variación de la velocidad con respecto al tiempo. Pudiendo ser este cambio en la magnitud(rapidez), en la dirección o en ambos.
Las variables que entran en juego (con sus respectivas unidades de medida) al estudiar este tipo de movimiento son:
Velocidad inicial Vo (m/s)
Velocidad final Vf (m/s)
Aceleración a (m/s2)
Tiempo t (s)
Distancia d (m)
Para efectuar cálculos que permitan resolver problemas usaremos las siguientes fórmulas:
Consejos o datos para resolver problemas:
La primera condición será obtener los valores numéricos de tres de las cinco variables. Definir la ecuación que refleje esas tres variables. Despejar y resolver numéricamente la variable desconocida.
Tener cuidado con que en algunas ocasiones un dato puede venir disfrazado; por ejemplo:
"un móvil que parte del reposo.....", significa que su velocidad inicial es Vo = 0 ; "en una prueba de frenado...", significa que su velocidad final es Vf = 0.
Veamos un problema como ejemplo
 |
En dirección hacia el sur, un tren viaja inicialmente a 16m/s; si recibe una aceleración constante de 2 m/s2. ¿Qué tan lejos llegará al cabo de 20 s.? ¿Cuál será su velocidad final en el mismo tiempo?
Veamos los datos que tenemos:
Conocemos tres de las cinco variables, entonces, apliquemos las fórmulas:
Averigüemos primero la distancia que recorrerá durante los 20 segundos:
Conozcamos ahora la velocidad final del tren, transcurridos los 20 segundos:
Respuestas:
Si nuestro tren, que viaja a 16 m/s, es acelerado a 2 m/s recorrerá 720 metros durante 20 segundos y alcanzará una velocidad de 56 m/s.
Movimiento rectilíneo uniformemente retardado
En los movimientos uniformemente decelerados o retardados la velocidad disminuye con el tiempo a ritmo constante. Están, pues, dotados de una aceleración que aunque negativa es constante. De ahí que todas las fórmulas usadas para los movimientos uniformemente acelerados sirvan para describir los movimientos uniformemente retardados, considerando sólo que su signo es negativo.
Por lo tanto, para efectuar cálculos que permitan resolver problemas que involucren aceleración negativa o deceleración, usaremos las siguientes fórmulas:
MOVIMIENTO DE CAÍDA LIBRE
 |
| Torre de experimentación para caída libre de cierta cantidad de átomos, en Bremen, Alemania. |
El movimiento de los cuerpos en caída libre (por la acción de su propio peso) es una forma derectilíneo uniformemente acelerado.
La distancia recorrida (d) se mide sobre la vertical y corresponde, por tanto, a una altura que se representa por la letra h.
En el vacío el movimiento de caída es de aceleración constante, siendo dicha aceleración la misma para todos los cuerpos, independientemente de cuales sean su forma y su peso.
La presencia de aire frena ese movimiento de caída y la aceleración pasa a depender entonces de la forma del cuerpo. No obstante, para cuerpos aproximadamente esféricos, la influencia del medio sobre el movimiento puede despreciarse y tratarse, en una primera aproximación, como si fuera decaída libre.
La aceleración en los movimientos de caída libre, conocida como aceleración de la gravedad, se representa por la letra g y toma un valor aproximado de 9,81 m/s2 (algunos usan solo el valor 9,8 o redondean en 10).
Si el movimiento considerado es de descenso o de caída, el valor de g resulta positivo como corresponde a una auténtica aceleración. Si, por el contrario, es de ascenso en vertical el valor deg se considera negativo, pues se trata, en tal caso, de un movimiento decelerado.
Para resolver problemas con movimiento de caída libre utilizamos las siguientes fórmulas:
 |
| Gota de agua en caída libre. |
Algunos datos o consejos para resolver problemas de caída libre:
Recuerda que cuando se informa que “Un objeto se deja caer” la velocidad inicial será siempre igual a cero (v0 = 0).
En cambio, cuando se informa que “un objeto se lanza” la velocidad inicial será siempre diferente a cero (vo ≠ 0).
Desarrollemos un problema para ejercitarnos
Desde la parte alta de este moderno edificio se deja caer una pelota, si tarda 3 segundos en llegar al piso ¿cuál es la altura del edificio? ¿Con qué velocidad impacta contra el piso?
 |
| Desde lo alto dejamos caer una pelota. |
Veamos los datos de que disponemos:
Para conocer la velocidad final (vf), apliquemos la fórmula
Ahora, para conocer la altura (h) del edificio, aplicamos la fórmula:
Respuestas:
La pelota se deja caer desde una altura de 44,15 metros e impacta en el suelo con una velocidad de 29,43 metros por segundo.
 |
Movimiento de subida o de tiro vertical
Al igual que la caída libre, este es un movimiento uniformemente acelerado.
Tal como la caída libre, es un movimiento sujeto a la aceleración de la gravedad (g), sólo que ahora la aceleración se opone al movimiento inicial del objeto.
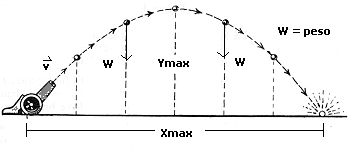
A diferencia de la caída libre, que opera solo de bajada, el tiro vertical comprende subida y bajada de los cuerpos u objetos y posee las siguientes características:
- La velocidad inicial siempre es diferente a cero.
- Mientras el objeto sube, el signo de su velocidad (V) es positivo.
- Su velocidad es cero cuando el objeto alcanza su altura máxima.
- Cuando comienza a descender, su velocidad será negativa.
- Si el objeto tarda, por ejemplo, 2 s en alcanzar su altura máxima, tardará 2 s en regresar a la posición original, por lo tanto el tiempo que permaneció en el aire el objeto es 4 s.
- Para la misma posición del lanzamiento la velocidad de subida es igual a la velocidad de bajada.
Para resolver problemas con movimiento de subida o tiro vertical utilizamos las siguientes fórmulas:
Primero necesitamos calcular (conocer) la velocidad inicial (V0), para ello usamos la fórmula
Ahora, para conocer el tiempo que demora el objeto en llegar a velocidad cero (altura máxima = 45 m) utilizamos la fórmula
Se define como movimiento circular aquél cuya trayectoria es una circunferencia.
 |
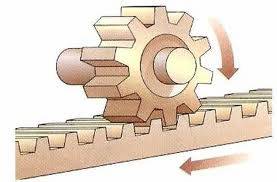| El movimiento circular del piñón se transforma en movimiento lineal en la cremallera. |
El movimiento circular, llamado también curvilíneo, es otro tipo de movimiento sencillo.
Estamos rodeados por objetos que describen movimientos circulares: un disco compacto durante su reproducción en el equipo de música, las manecillas de un reloj o las ruedas de una motocicleta son ejemplos de movimientos circulares; es decir, de cuerpos que se mueven describiendo una circunferencia.
A veces el movimiento circular no es completo: cuando un coche o cualquier otro vehículo toma una curva realiza un movimiento circular, aunque nunca gira los 360º de la circunferencia.
La experiencia nos dice que todo aquello da vueltas tiene movimiento circular. Si lo que gira da siempre el mismo número de vueltas por segundo, decimos que posee movimiento circular uniforme (MCU).
Ejemplos de cosas que se mueven con movimiento circular uniforme hay muchos:
La tierra es uno de ellos. Siempre da una vuelta sobre su eje cada 24 horas. También gira alrededor del sol y da una vuelta cada 365 días. Un ventilador, un lavarropas o los viejos tocadiscos, la rueda de un auto que viaja con velocidad constante, son otros tantos ejemplos.
Pero no debemos olvidar que también hay objetos que giran con movimiento circular variado, ya sea acelerado o decelerado.
El movimiento circular en magnitudes angulares
La descripción de un movimiento circular puede hacerse bien en función de magnitudes lineales ignorando la forma de la trayectoria (y tendremos velocidad y aceleración tangenciales), o bien en función de magnitudes angulares (y tendremos velocidad y aceleración angulares). Ambas descripciones están relacionadas entre sí mediante el valor del radio de la circunferencia trayectoria.
Al trabajar con magnitudes angulares es imprescindible entender lo relativo a una unidad de medida angular conocida como radián.
 |
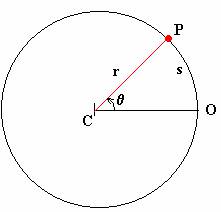| Ángulo θ con centro en C. |
El radián
Si tenemos un ángulo cualquiera y queremos saber cuánto mide, tomamos un transportador y lo medimos. Esto nos da el ángulo medido en grados. Este método viene de dividir la circunferencia en 360º, y se denomina sexagesimal.
(Para usar la calculadora en grados hay que ponerla en DEG, Degrees, que quiere decir grados en inglés).
El sistema de grados sexagesimales es una manera de medir ángulos, pero hay otros métodos, y uno de ellos es usando radianes.
Ahora veamos el asunto de medir los ángulos pero en radianes.
Para medir un ángulo en radianes se mide el largo del arco (s) abarcado por el ángulo θ de la figura a la izquierda. Esto se puede hacer con un centímetro, con un hilito o con lo que sea. También se mide el radio del círculo.
Para obtener el valor del ángulo (θ) en radianes usamos la fórmula:
y tenemos el ángulo medido en radianes
Hacer la división del arco sobre radio significa ver cuántas veces entra el radio en el arco. Como el radio y el arco deben medirse en la misma unidad, el radián resulta ser un número sin unidades.
Esto significa que el valor del ángulo en radianes solo me indica cuántas veces entra el radio en el arco. Por ejemplo, si el ángulo θ mide 3 radianes, eso significa que el radio entra 3 veces en el arco abarcado por ese ángulo.
Su quisiéramos calcular o conocer al valor del arco, hacemos:
 |
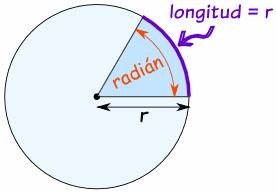| ¿Cuántas veces entra el radio en el arco marcado? |
¿A cuántos grados equivale un radián?
Pero el valor de un ángulo en radianes se puede expresar (convertir) en grados. En una circunferencia entera (360º) el arco entero es el perímetro, que es igual a 2 Pi por radio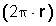 
. Así, a partir de la fórmula
es que 360° equivalen a:
. Así, a partir de la fórmula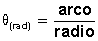es que 360° equivalen a:
Un ángulo de un radián equivale a un ángulo de 57,3º.
Para usar la calculadora en radianes hay que ponerla en "RAD"
Periodo y frecuencia
La principal característica del movimiento circular uniforme es que en cada vuelta o giro completo de 360°, equivalente a un ciclo, se puede establecer un punto fijo como inicio y fin del ciclo.
En física, los ciclos son también llamados revoluciones para un determinado tiempo.
El periodo (T) de un movimiento circular es el tiempo que tarda una partícula o un cuerpo en realizar una vuelta completa, revolución o ciclo completo.
Por ejemplo, el periodo de rotación de la tierra es 24 horas. El periodo de rotación de la aguja grande del reloj es de 1 hora. La unidad utilizada para el periodo es el segundo o, para casos mayores, unidades mayores.
Conocida la frecuencia (en ciclos o revoluciones por segundo) se puede calcular el periodo (T) mediante la fórmula:
Se denomina frecuencia (F) de un movimiento circular al número de revoluciones, vueltas o ciclos completos durante la unidad de tiempo. La unidad utilizada para cuantificar (medir) la frecuencia de un movimiento es el hertz (Hz), que indica el número de revoluciones o ciclos por cada segundo.
Para su cálculo, usamos la fórmula
o hertz:
(En ocasiones se usa, en vez de hertz, seg −1 o s −1 ). Nótese que la frecuencia (F) es la inversa del periodo (T).
 |
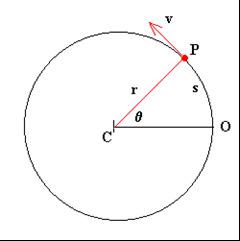| Imaginemos el punto rojo (P) como una piedra que gira amarrada al punto C. |
Una vez situado el origen O describimos el movimiento circular mediante las siguientes magnitudes angulares.
Posición angular (θ)
Podemos imaginar, como ejemplo, que se tiene una piedra amarrada a una cuerda y la movemos en círculos de radio r. En un instante de tiempo t el móvil (en nuestro caso la piedra) se encuentra en el punto P. Su posición angular (lo que la piedra ha recorrido en la circunferencia) viene dada por el ángulo θ, formado por el punto P, el centro de la circunferencia C y el origen O (desde donde empezó a girar la piedra).
La velocidad angular (ω)
Cuando un objeto se mueve en una circunferencia, llevará una velocidad, ya que recorre un espacio, pero también recorre un ángulo.
Para tener una idea de la rapidez con que algo se está moviendo con movimiento circular, se ha definido la velocidad angular (ω) como el número de vueltas que da el cuerpo por unidad de tiempo.
Si un cuerpo tiene gran velocidad angular quiere decir que da muchas vueltas por segundo.
Si un cuerpo tiene gran velocidad angular quiere decir que da muchas vueltas por segundo.
De manera sencilla: en el movimiento circular la velocidad angular está dada por la cantidad de vueltas que un cuerpo da por segundo.
Otra manera de decir lo mismo sería: en el movimiento circular la velocidad angular está dada por el ángulo recorrido (θ) dividido por unidad de tiempo. El resultado está en grados por segundo o en rad por segundo.
ω = velocidad angular en rad/seg.
θ = desplazamiento angular en rad.
t = tiempo en segundos en que se efectuó el desplazamiento angular.
La velocidad angular también se puede determinar si sabemos el tiempo que tarda en dar una vuelta completa o periodo (T):
Como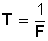
entonces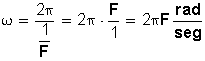 
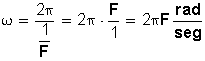
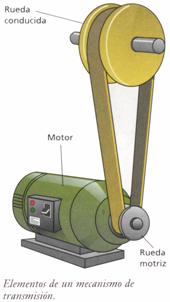entonces  |
| Trasmisión de un movimiento circular. |
Aquí debemos apuntar que una misma velocidad angular se puede expresar de varias maneras diferentes.
Por ejemplo, para las lavadoras automáticas o para los motores de los autos se usan lasrevoluciones por minuto (rpm). También a veces se usan las rps (revoluciones por segundo).
También se usan los grados por segundo y los radianes por segundo.
Es decir, hay muchas unidades diferentes de velocidad angular. Todas se usan y hay que saber pasar de una a otra, lo que se hace aplicando una regla de 3 simple.
Por ejemplo, pasar una velocidad de 60 rpm a varias unidades diferentes:
La más importante de todas las unidades de velocidad angular es radianes por segundo. Esta unidad es la que se usa en los problemas.
Nota importante:
Según lo anterior es correcto, entonces, decir que la velocidad angular es
, pero resulta que el radián es sólo un número comparativo, por lo mismo que la palabra radián suele no ponerse y en la práctica la verdadera unidad es
, que también puede ponerse como 
, e incluso como 
.En efecto, muchas veces la velocidad angular se expresa en segundos elevado a menos uno (
) y para quienes no lo saben resulta incomprensible.
La velocidad tangencial (v)
Aparte de la velocidad angular, también es posible definir la velocidad lineal de un móvil que se desplaza en círculo.
Por ejemplo, imaginemos un disco que gira. Sobre el borde del disco hay un punto que da vueltas con movimiento circular uniforme.
Ese punto tiene siempre una velocidad lineal que es tangente a la trayectoria. Esa velocidad se llama velocidad tangencial.
Para calcular la velocidad tangencial hacemos: espacio recorrido sobre la circunferencia (o arco recorrido) dividido por el tiempo empleado, que expresamos con la fórmula:
pero como 
entonces 
que se lee velocidad tangencial es igual a velocidad angular multiplicada por el radio.
Como la velocidad angular (ω) también se puede calcular en función del periodo (T) con la fórmula 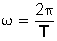y la velocidad tangencial siempre está en función del radio, entonces la fórmula se convierte en 
que se lee: la velocidad tangencial es igual a 2 pi multiplicado por el radio (r) y dividido por el periodo (T).
y la velocidad tangencial siempre está en función del radio, entonces la fórmula 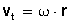se convierte en 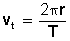que se lee: la velocidad tangencial es igual a 2 pi multiplicado por el radio (r) y dividido por el periodo (T).
Ver: PSU: Física; Pregunta 08_2005(2)
Además, como ω (velocidad angular) se expresa en y el radio se expresa en metros, las unidades de la velocidad tangencial serán metros por segundo (m/seg).
y el radio se expresa en metros, las unidades de la velocidad tangencial serán metros por segundo (m/seg). |
| Las ruedas se mueven con movimiento circular. |
La aceleración en los movimientos curvilíneos
En los movimientos curvilíneos o circulares la dirección cambia a cada instante. Y debemos recordar que la velocidad considerada como vectorv podrá variar (acelerar o decelerar) cuando varíe sólo su dirección, sólo su módulo o, en el caso más general, cuando varíen ambos.
La aceleración asociada a los cambios en dirección
En razón de la aseveración anterior, y desde un punto de vista sectorial (distancia), un movimiento circular uniforme es también un movimiento acelerado, aun cuando el móvil recorra la trayectoria a ritmo constante.
La dirección del vector velocidad, que es tangente a la trayectoria, va cambiando a lo largo del movimiento, y esta variación de v que afecta sólo a su dirección da lugar a una aceleración, llamada aceleración centrípeta.
Aceleración centrípeta
Cuando se estudió la aceleración en el movimiento rectilíneo, dijimos que ella no era más que el cambio constante que experimentaba la velocidad por unidad de tiempo. En este caso, la velocidad cambiaba únicamente en valor numérico (su módulo o rapidez), no así en dirección.
Ahora bien, cuando el móvil o la partícula realiza un movimiento circular uniforme, es lógico pensar que en cada punto el valor numérico de la velocidad (su módulo) es el mismo, en cambio es fácil darse cuenta de que la dirección del vector velocidad va cambiando a cada instante.
La variación de dirección del vector lineal origina una aceleración que llamaremos aceleración centrípeta. Esta aceleración tiene la dirección del radio y apunta siempre hacia el centro de la circunferencia.
Como deberíamos saber, cuando hay un cambio en alguno de los componentes del vector velocidad tiene que haber unaaceleración. En el caso del movimiento circular esa aceleración se llama centrípeta, y lo que la provoca es el cambio de dirección del vector velocidad angular.
 |
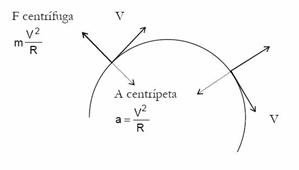| Aceleración centrípeta. |
Veamos el dibujo de la derecha:
El vector velocidad tangencial cambia de dirección y eso provoca la aparición de una aceleración que se llama aceleración centrípeta, que apunta siempre hacia el centro.
La aceleración centrípeta se calcula por cualquiera de las siguientes dos maneras:
La aceleración asociada a los cambios en su módulo (rapidez)
Ya sabemos que un movimiento circular, aunque sea uniforme, posee la aceleración centrípeta debida a los cambios de dirección que experimenta su vector velocidad. Ahora bien, si además la velocidad del móvil varía en su magnitud (módulo) diremos que además posee aceleración angular.
Resumiendo: si un móvil viaja en círculo con velocidad variable, su aceleración se puede dividir en dos componentes: una aceleración de la parte radial (la aceleración centrípeta que cambia la dirección del vector velocidad) y una aceleración angular que cambia la magnitud del vector velocidad, además de una aceleración tangencial si consideramos solo su componente lineal. (Ver:Rapidez y velocidad).
Como corolario, podemos afirmar que un movimiento circular uniforme posee solo aceleración centrípeta y que un movimiento circular variado posee aceleración centrípeta y, además, aceleraciones angular y tangencial.
Aceleración angular
Tal como el movimiento lineal o rectilíneo, el movimiento circular puede ser uniforme o acelerado. La rapidez de rotación puede aumentar o disminuir bajo la influencia de un momento de torsión resultante.
La aceleración angular (α) se define como la variación de la velocidad angular con respecto al tiempo y está dada por:
donde:
α = aceleración angular final en rad/ s2
ωf = velocidad angular final en rad/s
ωi = velocidad angular inicial en rad/s
t = tiempo transcurrido en seg
Una forma más útil de la ecuación anterior es:
ωf = ωi + α t
Aceleración tangencial
Imaginemos de nuevo un disco que gira. Sobre el borde del disco hay un punto que da vueltas con movimiento circular acelerado.
Ese punto tiene siempre una velocidad variada que es tangente a la trayectoria. Esa variación de velocidad se llama aceleración tangencial.
Es la aceleración que representa un cambio en la velocidad lineal, y se expresa con la fórmula
Donde
α = valor de la aceleración angular en rad/s2
r = radio de la circunferencia en metros (m)
Entonces, la aceleración tangencial es igual al producto de la aceleración angular por el radio.
Otras fórmulas usadas en el movimiento circular
Vimos que la velocidad angular (ω) es igual al ángulo recorrido dividido por el tiempo empleado. Cuando el tiempo empleado sea justo un período (T), el ángulo recorrido será 2 pi (igual a una vuelta).
Entonces podemos calcular la velocidad angular (ω) como:
Pero como 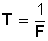, esta misma fórmula se puede poner como:
, esta misma fórmula se puede poner como:
Ejercicios sobre movimiento circular uniforme
Ejercicio 1)
Un móvil con trayectoria circular recorrió 820° ¿Cuántos radianes son?
Desarrollo
Sabemos que 1 rad = 57,3°
Entonces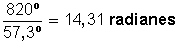 
Ejercicio 2)
 |
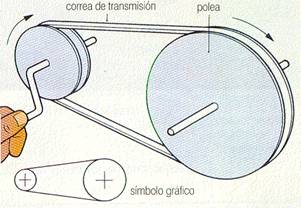| Como en un tractor, la rueda delantera es más chica. |
Un tractor tiene una rueda delantera de 30 cm de radio, mientras que el radio de la trasera es de 1 m. ¿Cuántas vueltas habrá dado la rueda trasera cuando la delantera ha completado 15 vueltas?
Desarrollo:
En este ejercicio la longitud (distancia, espacio) que recorre cada rueda en una vuelta corresponde al perímetro de cada una (perímetro del círculo), cuya fórmula es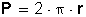 
, entonces:
, entonces:
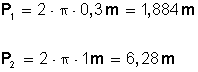
Entonces, si en una vuelta la rueda delantera recorre 1,884 metro, en 15 vueltas recorrerá: 15 • 1,884 m = 28,26 m
¿Cuantas veces la rueda trasera ha tenido que girar (dar una vuelta) para recorrer esa distancia de 28,26 m?
Dividimos esa distancia por la distancia recorrida en una vuelta por la rueda trasera:
28,26 m : 6,28 m = 4,5 vueltas.
Por lo tanto, la rueda trasera ha tenido que dar cuatro vueltas y media para recorrer la misma distancia que la delantera ha recorrido en 15 vueltas.
Ejercicios sobre el movimiento circular variado (acelerado)
Ejercicio 1)
Un automóvil, cuyo velocímetro indica en todo instante 72 km/h, recorre el perímetro de una pista circular en un minuto. Determinar el radio de la misma. Si el automóvil tiene una aceleración en algún instante, determinar su módulo, dirección y sentido.
Si la pista es circular, la velocidad que tiene el auto es la velocidad tangencial. Si da una vuelta a la pista en un minuto, significa que su periodo (T) es de un minuto.
Ahora, como 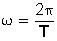, entonces:
velocidad angular .
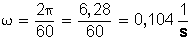, entonces: velocidad angular .
Por otro lado, la velocidad tangencial es 20 m/s (72 km/h), reemplazando en la fórmula:
Tenemos
Calculamos r:
R = 192 m Radio de la pista
Ahora, aunque su velocidad (rapidez) sea constante, igual tiene aceleración centrípeta, cuyo módulo es
Aceleración centrípeta, dirigida hacia el centro de la pista.
Ejercicio 2)
Un automóvil recorre la circunferencia de 50 cm de radio con una frecuencia F de 10 hz.
Determinar:
a) el periodo.
b) la velocidad angular.
c) su aceleración.
Una frecuencia de 50 hz es una frecuencia de 50 1/s. Para su desarrollo, sólo debemos aplicar formulas.
Sabemos que
, entonces
, velocidad angular (039)El período T es
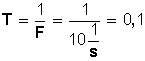s (Período)Conocemos la velocidad angular y el radio, podemos calcular la velocidad tangencial:
, velocidad tangencial.
Su aceleración va a ser la aceleración centrípeta, que siempre esta apuntando hacia el centro de la circunferencia. El módulo de esta aceleración se puede calcular por cualquiera de las siguientes dos fórmulas:
Usando la segunda:
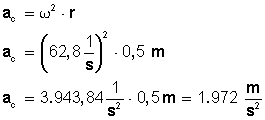
Ejercicio 3)
¿Cuál es la aceleración que experimenta un niño que viaja en el borde de un carrusel que tiene 2 m de radio y que da una vuelta cada 8 segundos?
Si el niño da 1 vuelta cada 8 segundos su velocidad angular va a ser:
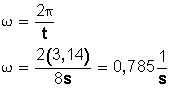
Para calcular la aceleración centrípeta tenemos
Entonces:
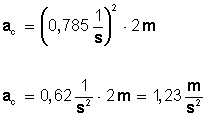
Es la aceleración centrípeta del niño.
Ejercicio 4)
Calcular la velocidad angular y la frecuencia con que debe girar una rueda, para que los puntos situados a 50 cm de su eje estén sometidos a una aceleración que sea 500 veces la de la gravedad.
Veamos los datos:
Necesitamos que la aceleración centrípeta sea igual a 500 g:
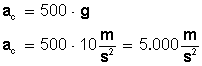
La velocidad angular para la cual se cumpla esto va a ser:
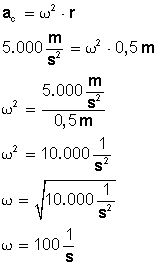
Ahora calculamos la frecuencia (F) a partir de
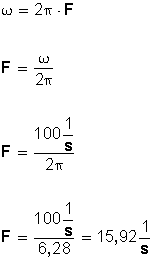
MOVIMIENTO CIRCULAR UNIFORMEMENTE VARIADO
En MCUV el móvil se desplaza sobre una circunferencia variando el módulo tanto de su velocidad angular como tangencial continuamente. Existen una aceleración tangencial y una aceleración angular, que modifican a las velocidades correspondientes.
ACELERACIÓN ANGULAR
Es la variación de la velocidad angular en el tiempo.
ACELERACIÓN TANGENCIAL
Es la variación de la velocidad tangencial en el tiempo.
VELOCIDADES EN EL MCUV
En MCUV las velocidades angulares y tangenciales no son constantes.
VELOCIDAD ANGULAR
Es la diferencia entre el ángulo final e incial, dividida por el tiempo. Se calcula sumando la velocidad angular inicial al producto de la aceleración angular por el tiempo (de manera similar a MRUV cuando se calcula la velocidad final). La ecuación se despeja de la definición de aceleración angular.
ACELERACIÓN ANGULAR
Es la variación de la velocidad angular en el tiempo.
ACELERACIÓN TANGENCIAL
Es la variación de la velocidad tangencial en el tiempo.
VELOCIDADES EN EL MCUV
En MCUV las velocidades angulares y tangenciales no son constantes.
VELOCIDAD ANGULAR
Es la diferencia entre el ángulo final e incial, dividida por el tiempo. Se calcula sumando la velocidad angular inicial al producto de la aceleración angular por el tiempo (de manera similar a MRUV cuando se calcula la velocidad final). La ecuación se despeja de la definición de aceleración angular.
VELOCIDAD TANGENCIAL
Es la diferencia entre la posición final e inicial, dividida por el tiempo. Se calcula sumando la velocidad tangencial inicial al producto de la aceleración tangencial por el tiempo (de manera similar a MRUV cuando se calcula la velocidad final).
En un determinado instante, si tenemos la velocidad angular, la velocidad tangencial se calcula de la misma manera que en MRU:
POSICIÓN RESPECTO DEL TIEMPO EN MUCV
Las ecuaciones horarias pueden ser planteadas tanto para las magnitudes tangenciales como para las angulares y son similares a las de MRUV. Si se trabaja con ángulos, al igual que en MCU, hay que restar un número entero k por 2 π (número de vueltas por ángulo de cada vuelta).
Es la diferencia entre la posición final e inicial, dividida por el tiempo. Se calcula sumando la velocidad tangencial inicial al producto de la aceleración tangencial por el tiempo (de manera similar a MRUV cuando se calcula la velocidad final).
En un determinado instante, si tenemos la velocidad angular, la velocidad tangencial se calcula de la misma manera que en MRU:
POSICIÓN RESPECTO DEL TIEMPO EN MUCV
Las ecuaciones horarias pueden ser planteadas tanto para las magnitudes tangenciales como para las angulares y son similares a las de MRUV. Si se trabaja con ángulos, al igual que en MCU, hay que restar un número entero k por 2 π (número de vueltas por ángulo de cada vuelta).
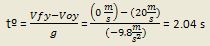
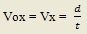
No hay comentarios.:
Publicar un comentario