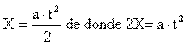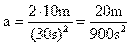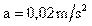La Energía es un concepto esencial de las ciencias. Desde un punto de vista material complejo de definir. La más básica de sus definiciones indica que se trata de la capacidad que poseen los cuerpos para producir Trabajo, es decir la cantidad de energía que contienen los cuerpos se mide por el trabajo que son capaces de realizar.
La realidad del mundo físico demuestra que la energía, siendo única, puede presentarse bajo diversas formas capaces de transformarse unas a otras.
Energía eléctrica
Se denomina energía eléctrica a la forma de energía que resulta de la existencia de una diferencia de potencial entre dos puntos, lo que permite establecer una corriente eléctrica entre ambos (cuando se les coloca en contacto por medio de un conductor eléctrico) para obtener trabajo.

Energía luminosa
La energía lumínica o luminosa es la energía fracción percibida de la energía transportada por la luz y que se manifiesta sobre la materia de distintas maneras, una de ellas es arrancar los electrones de los metales, puede comportarse como una onda o como si fuera materia, pero lo más normal es que se desplace como una onda e interactúe con la materia de forma material o física.
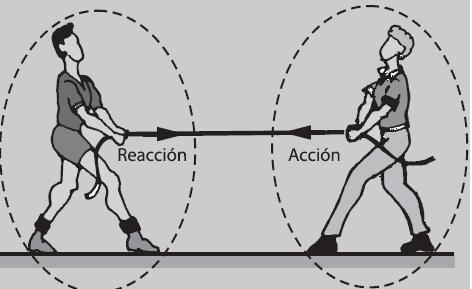
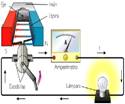
Energía mecánica
La energía mecánica es la energía que se debe a la posición y al movimiento de un cuerpo, por lo tanto, es la suma de las energías potencial, cinética y la energía elástica de un cuerpo en movimiento. Expresa la capacidad que poseen los cuerpos con masa de efectuar un trabajo.
Energía térmica
Se denomina energía térmica a la energía liberada en forma de calor. Puede ser obtenida de la naturaleza, a partir de la energía térmica, mediante una reacción exotérmica, como la combustión de algún combustible; por una reacción nuclear de fisión o de fusión; mediante energía eléctrica por efecto Joule o por efecto termoeléctrico; o por rozamiento, como residuo de otros procesos mecánicos o químicos. Asimismo, es posible aprovechar energía de la naturaleza que se encuentra en forma de energía térmica, como la energía geotérmica o la energía solar fotovoltaica.
La energía térmica se puede transformar utilizando un motor térmico, ya sea en energía eléctrica, en una central termoeléctrica; o en trabajo mecánico, como en un motor de automóvil, avión o barco.
La obtención de energía térmica implica un impacto ambiental. La combustión libera dióxido de carbono (CO2) y emisiones contaminantes. La tecnología actual en energía nuclear da lugar a residuos radiactivos que deben ser controlados. Además deben tenerse en cuenta la utilización de terreno de las plantas generadoras de energía y los riesgos de contaminación por accidentes en el uso de los materiales implicados, como los derrames de petróleo o de productos petroquímicos derivados.

Energía eólica
Energía eólica es la energía obtenida del viento, es decir, la energía cinética generada por efecto de las corrientes de aire, y que es transformada en otras formas útiles para las actividades humanas.
El término eólico viene del latín Aeolicus, perteneciente o relativo a Eolo, dios de los vientos en la mitología griega. La energía eólica ha sido aprovechada desde la antigüedad para mover los barcos impulsados por velas o hacer funcionar la maquinaria de molinos al mover sus aspas.
En la actualidad, la energía eólica es utilizada principalmente para producir energía eléctrica mediante aerogeneradores. A finales de 2007, la capacidad mundial de los generadores eólicos fue de 94.1 gigavatios.1 Mientras la eólica genera alrededor del 1% del consumo de electricidad mundial,2 representa alrededor del 19% de la producción eléctrica en Dinamarca, 9% en España y Portugal, y un 6% en Alemania e Irlanda (Datos del 2007). En el año 2008 el porcentaje aportado por la energía eólica en España aumentó hasta el 11%.3
La energía eólica es un recurso abundante, renovable, limpio y ayuda a disminuir las emisiones de gases de efecto invernadero al reemplazar termoeléctricas a base de combustibles fósiles, lo que la convierte en un tipo de energía verde. Sin embargo, el principal inconveniente es su intermitencia.

Energía solar
La energía solar es la energía obtenida mediante la captación de la luz y el calor emitidos por el Sol.
La radiación solar que alcanza la Tierra puede aprovecharse por medio del calor que produce a través de la absorción de la radiación, por ejemplo en dispositivos ópticos o de otro tipo. Es una de las llamadas energías renovables, particularmente del grupo no contaminante, conocido como energía limpia o energía verde. Si bien, al final de su vida útil, los paneles fotovoltaicos pueden suponer un residuo contaminante difícilmente reciclable al día de hoy.
La potencia de la radiación varía según el momento del día, las condiciones atmosféricas que la amortiguan y la latitud. Se puede asumir que en buenas condiciones de irradiación el valor es de aproximadamente 1000 W/m² en la superficie terrestre. A esta potencia se la conoce como irradiancia.
La radiación es aprovechable en sus componentes directa y difusa, o en la suma de ambas. La radiación directa es la que llega directamente del foco solar, sin reflexiones o refracciones intermedias. La difusa es la emitida por la bóveda celeste diurna gracias a los múltiples fenómenos de reflexión y refracción solar en la atmósfera, en las nubes y el resto de elementos atmosféricos y terrestres. La radiación directa puede reflejarse y concentrarse para su utilización, mientras que no es posible concentrar la luz difusa que proviene de todas las direcciones.
La irradiancia directa normal fuera de la atmósfera, recibe el nombre de constante solar y tiene un valor medio de 1354 W/m² (que corresponde a un valor máximo en el perihelio de 1395 W/m² y un valor mínimo en el afelio de 1308 W/m²).
Según informes de Greenpeace, la energía solar fotovoltaica podría suministrar electricidad a dos tercios de la población mundial en 2030.1

Energía nuclear
La energía nuclear es aquella que se libera como resultado de una reacción nuclear. Se puede obtener por el proceso de Fisión Nuclear (división de núcleos atómicos pesados) o bien por Fusión Nuclear (unión de núcleos atómicos muy livianos). En las reacciones nucleares se libera una gran cantidad de energía debido a que parte de la masa de las partículas involucradas en el proceso, se transforma directamente en energía. Lo anterior se puede explicar basándose en la relación Masa-Energía producto de la genialidad del gran físico Albert Einstein.

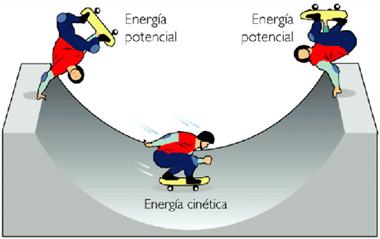
Energía cinética
Energía que un objeto posee debido a su movimiento. La energía cinética depende de la masa y la velocidad del objeto según la ecuación E = 1mv2, donde m es la masa del objeto y v2 la velocidad del mismo elevada al cuadrado. La energía asociada a un objeto situado a determinada altura sobre una superficie se denomina energía potencial. Si se deja caer el objeto, la energía potencial se convierte en energía cinética.

Energía potencial
La energía potencial es la capacidad que tienen los cuerpos para realizar un trabajo, dependiendo de la configuración que tengan en un sistema de cuerpos que ejercen fuerzas entre sí. Puede pensarse como la energía almacenada en un sistema, o como una medida del trabajo que un sistema puede entregar. Más rigurosamente, la energía potencial es una magnitud escalar asociada a un campo de fuerzas (o como enelasticidad un campo tensorial de tensiones). Cuando la energía potencial está asociada a un campo de fuerzas, la diferencia entre los valores del campo en dos puntos A y B es igual al trabajo realizado por la fuerza para cualquier recorrido entre B y A.
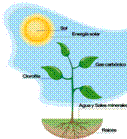
Energía química
La energía química es la energía acumulada en los alimentos y en los combustibles. Se produce por la transformación de sustancias químicas que contienen los alimentos o elementos, posibilita mover objetos o generar otro tipo de energía.

Energía hidráulica
Se denomina energía hidráulica o energía hídrica a aquella que se obtiene del aprovechamiento de las energías cinética y potencial de la corriente de ríos, saltos de agua o mareas. Es un tipo de energía verde cuando su impacto ambiental es mínimo y usa la fuerza hídrica sin represarla, en caso contrario es considerada sólo una forma de energía renovable.

Energía sonora
La energía sonora es aquella que se produce con la vibración o el movimiento de un objeto, que hace vibrar también el aire que lo rodea y esa vibración se transforma en impulsos eléctricos que en el cerebro se interpretan como sonidos.

Energía radiante
Es la energía que poseen las ondas electromagnéticas como la luz visible, las ondas de radio, los rayos ultravioletas (UV), los rayos infrarrojos (IR), etc. La característica principal de esta energía es que se propaga en el vacío sin necesidad de soporte material alguno. Se transmite por unidades llamadas fotones, estas unidades llamadas fotones actúan también como partículas, debe ser como lo plantease el físico Albert Einstein en su teoría de la relatividad general.

Energía fotovoltaica
Los sistemas de energía fotovoltaica permiten la transformación de la luz solar en energía eléctrica, es decir, la conversión de una partícula luminosa con energía (fotón) en una energía electromotriz (voltaica).
El elemento principal de un sistema de energía fotovoltaica es la célula fotoeléctrica, un dispositivo construido de silicio (extraído de la arena común).

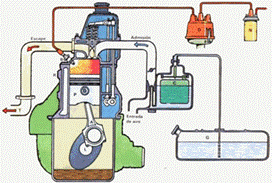
Energía de reacción
En una reacción química el contenido energético de los productos es, en general, diferente del correspondiente a los reactivos. Este defecto o exceso de energía es el que se pone en juego en la reacción. La energía desprendida o absorbida puede ser en forma de energía luminosa, eléctrica, mecánica, etc.. pero habitualmente se manifiesta en forma de calor. El calor intercambiado en una reacción química se llama calor de reacción y tiene un valor característico para cada reacción. Las reacciones pueden entonces clasificarse en exotérmicas o endotérmicas, según que haya desprendimiento o absorción de calor.
Energía iónica
La energía de ionización es la cantidad de energía que se necesita para separar el electrón menos fuertemente unido de un átomo neutro gaseoso en su estado fundamental.
El petróleo como energía
Es un recurso natural no renovable y actualmente también es la principal fuente de energía en los países desarrollados. El petróleo líquido puede presentarse asociado a capas de gas natural, en yacimientos que han estado enterrados durante millones de años, cubiertos por los estratos superiores de la corteza terrestre.

El gas natural como energía
El gas natural es una fuente de energía no renovable formada por una mezcla de gases que se encuentra frecuentemente en yacimientos de petróleo, disuelto o asociado con el petróleo o en depósitos de carbón. Aunque su composición varía en función del yacimiento del que se extrae, está compuesto principalmente por metano en cantidades que comúnmente pueden superar el 90 ó 95%, y suele contener otros gases como nitrógeno, CO2, H2S, helio y mercaptanos.

El carbón como energía
El carbón es un tipo de roca formada por el elemento químico carbono mezclado con otras sustancias. Es una de las principales fuentes de energía. En 1990, por ejemplo, el carbón suministraba el 27,2% de la energía comercial del mundo.

Energía geotérmica
La energía geotérmica es aquella energía que puede ser obtenida por el hombre mediante el aprovechamiento del calor del interior de la Tierra. El calor del interior de la Tierra se debe a varios factores, entre los que caben destacar el gradiente geotérmico, el calor radiogénico, etc. Geotérmico viene del griego geo, "Tierra", y thermos, "calor"; literalmente "calor de la Tierra".

Leer más: http://www.monografias.com/trabajos84/tipos-energia/tipos-energia.shtml#ixzz4CprKEg70
.jpg/260px-Sir_Isaac_Newton_(1643-1727).jpg)