Gasto o Caudal

Teorema de Bernoulli

Teorema de Bernoulli

En todo fluido ideal (sin viscosidad ni rozamiento), incomprensible, en régimen laminar de circulación por un conducto cerrado, la energía que posee el fluido permanece constante a lo largo de todo su recorrido.

El teorema de Bernoulli es una aplicación directa del principio de conservación de energía. Con otras palabras está diciendo que si el fluido no intercambia energía con el exterior (por medio de motores, rozamiento, térmica...) esta ha de permancer constante.

El teorema considera los tres unicos tipos de energía que posee el fluido que pueden cambiar de un punto a otro de la conducción. Estos tipos son; energía cinética, energía potencial gravitatoria y la energía debida a la presión de flujo (hidroestática). Veamos cada una de ellas por separado:

Imagen 11. Speedace. Copyright

Energía cinética (hidrodinámica)	Debida a la velocidad de flujo
Energía potencial gravitatoria	Debida a la altitud del fluido
Energía de flujo (hidroestática)	Debida a la presión a la que está sometido el fluido

Por lo tanto el teorema de Bernoulli se expresa de la siguiente forma:

Donde:

• v es la velocidad de flujo del fluido en la sección considerada.
• g es la constante de gravedad.
• h es la altura desde una cota de referencia.
• p es la presión a lo largo de la línea de corriente del fluido (p minúscula).
• ρ es la densidad del fluido.

Si consideramos dos puntos de la misma conducción (1 y 2) la ecuación queda:

Donde m es constante por ser un sistema cerrado y V también lo es por ser un fluido icompresible. Dividiendo todos los términos por V, se obtiene la forma más común de la ecuación de Bernoulli, en función de la densidad del fluido:

Una simplifación que en muchos casos es aceptable es considerar el caso en que la altura es constante, entonces la expresión de la ecuación de Bernoulli, se convierte en:

Un ejemplo de aplicación del principio lo encontramos en el flujo de agua en una tubería de sección variable.

Imagen 12. mauuel. Copyright

Cuando el fluido se mueve hacia la derecha, la velocidad en el punto 2 es mayor que en el punto 1(ecuación de continuidad), por lo que la presión en 2 será menor que en 1, (ecuación de Bernouilli) la caída de presión determinan las diferencias de altura en las columnas h.

Una aplicación muy extendida del sistema anterior es el tubo de Venturi. Este sistema permite medir la velocidad de flujo de un fluido a través de una tubería utilizando un sistema como el de la figura:

Obtén la expresión teórica que permite calcular la velocidad de circulación en la tubería 1 en función de su diámetro, del diámetro del estrechamiento y de la longitud y dendisdad de la columna de líquido manométrico (h).

Como punto de partida toma:

- La ecuación de continuidad: 

- El teorema de Bernoulli simplificado para altura constante: 

Problemas.

1) En la figura, el fluido es agua y descarga libremente a la atmósfera. Para un flujo másico de 15 kg/s, determine la presión en el manómetro.

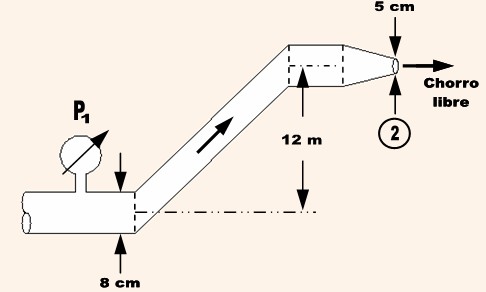
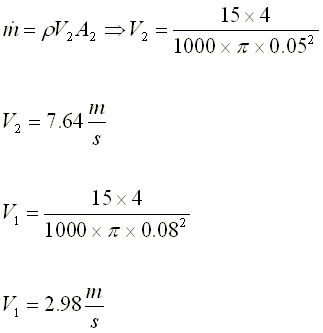
Aplicando la e.c de Bernoulli entre 1 y 2 tenemos

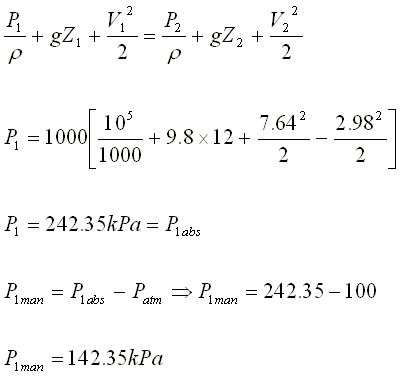
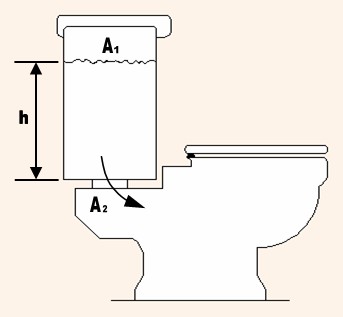
2) El tanque de una poceta tiene una sección rectangular de dimensiones 20cmx40cm y el nivel del agua está a una altura  

h = 20 cm  por encima de la válvula de desagüe, la cual tiene un diámetro d₂ = 5 cm. Si al bajar la palanca, se abre la válvula:

a) ¿Cuál será la rapidez inicial de desagüe por esa válvula en función de la altura de agua remanente en el tanque?

b) ¿Cuál es la rapidez inicial de desagüe? No desprecie la velocidad en la superficie del tanque.

Aplicando la ecuación de Bernoulli

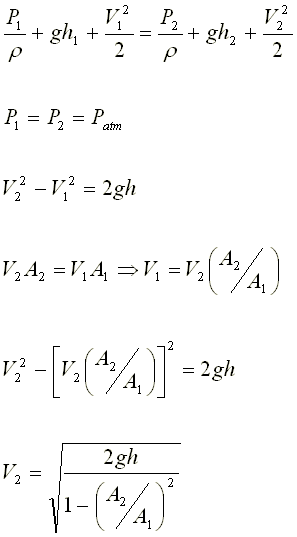
Calculamos la rapidez

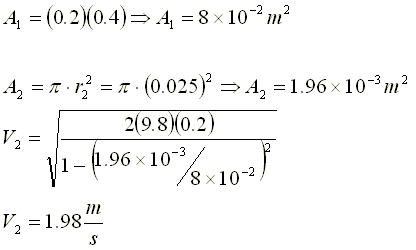
Gasto o Caudal

Gasto o Caudal

• En dinámica de fluidos, caudal es la cantidad de fluido que avanza en una unidad de tiempo. Se denomina también caudal volumétrico o índice de flujo fluido, y que puede ser expresado en masa o en volumen. Caudalímetro: instrumento empleado para la medición del caudal de un fluido o gasto másico.Cálculo de caudal de agua en tubería: estimación del comportamiento de un flujo de tubería, basado en la ecuación de continuidad:En ecología, se denomina caudal al volumen de agua que arrastra un río, o cualquier otra corriente de agua para preservar los valores ecológicos en el cauce de la misma; se mide en metros cúbicos por segundo.

Asociado al término anterior:

• Caudal sólido: denominación para el material arrastrado por la corriente de agua.
• Caudal regularizado: determinación de la capacidad reguladora de un embalse.
• Régimen fluvial: se refiere a las variaciones en el caudal de un río a lo largo de un año.

La ecuación de continuidad se puede expresar como:
ρ1.A1.V1 = ρ2.A2.V2
Cuando ρ1 = ρ2, que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
[pic]
o de otra forma:
[pic](el caudal que entra es igual al que sale)
Donde:
• Q = caudal (metro cúbico por segundo; m3 / s)
• V = velocidad (m / s)
• A = area transversal del tubo de corriente o conducto (m2)