Circuito RLC
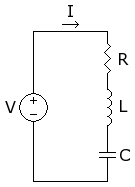
En electrodinámica un circuito RLC es un circuito lineal que contiene una resistencia eléctrica, una bobina (inductancia) y un condensador (capacitancia).
Existen dos tipos de circuitos RLC, en serie o en paralelo, según la interconexión de los tres tipos de componentes. El comportamiento de un circuito RLC se describe generalmente por una ecuación diferencial de segundo orden (en donde los circuitos RC o RL se comportan como circuitos de primer orden).
Con ayuda de un generador de señales, es posible inyectar en el circuito oscilaciones y observar en algunos casos el fenómeno de resonancia, caracterizado por un aumento de la corriente (ya que la señal de entrada elegida corresponde a la pulsación propia del circuito, calculable a partir de la ecuación diferencial que lo rige).
Circuito sometido a un escalón de tensión[editar]
Si un circuito RLC en serie es sometido a un escalón de tensión , la ley de las mallas impone la relación:
Introduciendo la relación característica de un condensador:
Se obtiene la ecuación diferencial de segundo orden:
Donde:
- E es la fuerza electromotriz de un generador, en Voltios (V);
- uC es la tensión en los bornes de un condensador, en Voltios (V);
- L es la inductancia de la bobina, en Henrios (H);
- i es la intensidad de corriente eléctrica en el circuito, en Amperios (A);
- q es la carga eléctrica del condensador, en Coulombs (C);
- C es la capacidad eléctrica del condensador, en Faradios (F);
- Rt es la resistencia total del circuito, en Ohmios (Ω);
- t es el tiempo en segundos (s)
En el caso de un régimen sin pérdidas, esto es para , se obtiene una solución de la forma:
Donde:
- T0 el periodo de oscilación, en segundos;
- φ la fase en el origen (lo más habitual es elegirla para que φ = 0)
Lo que resulta:
Donde es la frecuencia de resonancia, en hercios (Hz).
Circuitos sometidos a una tensión sinusoidal[editar]
La transformación compleja aplicada a las diferentes tensiones permite escribir la ley de las mallas bajo la forma siguiente:
siendo la tensión en el generador. Introduciendo las impedancias complejas:
![{\displaystyle {\underline {U_{G}}}=R{\underline {I}}+j\omega L{\underline {I}}-{\frac {j}{\omega C}}{\underline {I}}={\bigg [}R+j\ {\frac {\omega ^{2}LC-1}{\omega C}}{\bigg ]}{\underline {I}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9b03da02ee5e5166e3388022b5cd7ae99797777)
La frecuencia angular (o pulsación) de resonancia de corriente de este circuito ω0 es dada por:
Para esta frecuencia la relación de arriba se convierte en:
- y se obtiene:
No hay comentarios.:
Publicar un comentario